Advertisements
Advertisements
प्रश्न
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
उत्तर
In equilateral traingle all the angles are of 60°
∴ ∠ABO = ∠AOB = 60°
Area of the shaded region = (Area of tringle AOB - Area of sector having central angle 60°) +Area of sector having central angle (360° - 60°)
`= sqrt(3)/4("AB")^2 - 60^circ/360^circ pi (6)^2+(300°)/(360°)pi(6)^2`
`=1.73/4(12)^2-1/6xx3.14xx(6)^2+5/6xx3.14(6)^2`
=62.28-18.84 + 94.2
= 137.64 cm2
Hence, the area of shaded region is 137.64 cm2
APPEARS IN
संबंधित प्रश्न
Find the area of the following circle, given that diameter = 49 m.
Each of the equal sides of an isosceles triangle measure 2 cm more than its height, and the base of the triangle measure 12 cm. Find the area of the triangle.
The perimeter of a rectangular plot of land is 80 m and its breadth is 16 m. Find the length and area of the plot.
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
The area of a sector whose perimeter is four times its radius r units, is
The perimeter of a certain sector of a circle of radius 6.5 cm in 31 cm. Find the area of the sector.
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

The area of a circle is 98.56 cm2. Find its circumference.
The areas of two concentric circles are 1386 cm2 and 962.5 cm2. The width of the ring is
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.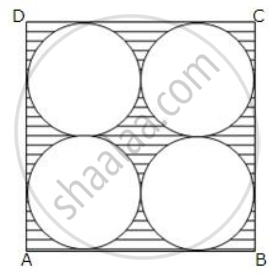
Find the area of the remaining card-board.
