Advertisements
Advertisements
Question
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
Solution
In equilateral traingle all the angles are of 60°
∴ ∠ABO = ∠AOB = 60°
Area of the shaded region = (Area of tringle AOB - Area of sector having central angle 60°) +Area of sector having central angle (360° - 60°)
`= sqrt(3)/4("AB")^2 - 60^circ/360^circ pi (6)^2+(300°)/(360°)pi(6)^2`
`=1.73/4(12)^2-1/6xx3.14xx(6)^2+5/6xx3.14(6)^2`
=62.28-18.84 + 94.2
= 137.64 cm2
Hence, the area of shaded region is 137.64 cm2
APPEARS IN
RELATED QUESTIONS
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14)
The adjacent sides of a parallelogram are 32 cm and 24 cm. If the distance between the longer sides is 17.4 cm, find the distance between the shorter sides.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
The area of sector is one-twelfth that of the complete circle. Find the angle of the sector .
In the following figure find the area of the shaded region. (Use π = 3.14)
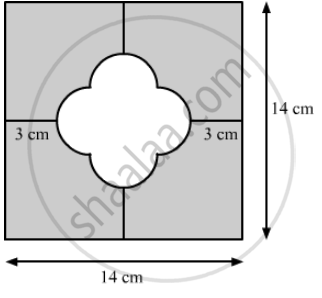
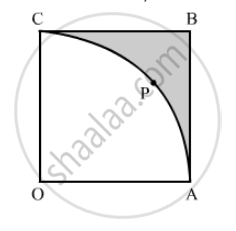
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
There is a path of uniform width 7 m round and outside a circular garden of diameter 210 m. Find the area of the path.
