Advertisements
Advertisements
Question
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

Solution
(i) Area of the shaded region can be calculated as shown below,
Area of the shaded region = Area of the semi-circle with diameter of 9 cm − area of 2 semi-circles with radius 3cm − area of the circle with centre D + area of semi-circle with radius 3 cm
`∴ "Area of the shaded region "=(pixx4.5xx4.5)/2-(2xxpixx1.5xx1.5)/2-pixx2.25xx2.25+(pixx1.5xx1.5)/2`
`"rea of the shaded region"= (pixx4.5xx4.5)/2-(pixx1.5xx1.5)/2-pixx2.25xx2.25`
`∴ "Area of the shaded region " pi/2(20.25-2.25)-pixx5.0625`
`∴" Area of the shaded region"=pi/2(18)-pixx5.0625 `
`∴" Area of the shaded region"=9pi-pixx5.0625`
`∴" Area of the shaded region"=pi(9-5.0625)`
`∴" Area of the shaded region"=3.9375 pi`
Substituting `pi=22/7 "we get"`
`∴" Area of the shaded region"=3.9375xx222/7`
`∴" Area of the shaded region"=12.375`
Therefore, area of the shaded region is`12.375 cm^2`
Now we will find the cost of painting the shaded region at the rate of 25 paise per cm2.
`∴ "Cost" =12.375xx25`
`∴ "Cost"=309.375` paise
`∴ "Cost"=Rs=3`
Therefore, cost of painting the shaded region to the nearest rupee is Rs `3`
APPEARS IN
RELATED QUESTIONS
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
The area of the incircle of an equilateral triangle of side 42 cm is
The hour hand of a clock is 6 cm long. The area swept by it between 11.20 am and 11.55 am is
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
The minute hand of a clock is 8 cm long. Find the area swept by the minute hand between 8.30 a.m. and 9.05 a.m.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.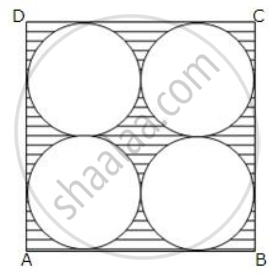
Find the area of the remaining card-board.
There is a path of uniform width 7 m round and outside a circular garden of diameter 210 m. Find the area of the path.
The diameter of a wheel is 0.70 m. Find the distance covered by it in 500 revolutions. If the wheel takes 5 minutes to make 500 revolutions; find its speed in :
(i) m/s
(ii) km/hr.
A pendulum swings through an angle of 30∘ and describes an arc 8.8 cm in length. Find the length of the pendulum in cm.
