Advertisements
Advertisements
प्रश्न
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

उत्तर
(i) Area of the shaded region can be calculated as shown below,
Area of the shaded region = Area of the semi-circle with diameter of 9 cm − area of 2 semi-circles with radius 3cm − area of the circle with centre D + area of semi-circle with radius 3 cm
`∴ "Area of the shaded region "=(pixx4.5xx4.5)/2-(2xxpixx1.5xx1.5)/2-pixx2.25xx2.25+(pixx1.5xx1.5)/2`
`"rea of the shaded region"= (pixx4.5xx4.5)/2-(pixx1.5xx1.5)/2-pixx2.25xx2.25`
`∴ "Area of the shaded region " pi/2(20.25-2.25)-pixx5.0625`
`∴" Area of the shaded region"=pi/2(18)-pixx5.0625 `
`∴" Area of the shaded region"=9pi-pixx5.0625`
`∴" Area of the shaded region"=pi(9-5.0625)`
`∴" Area of the shaded region"=3.9375 pi`
Substituting `pi=22/7 "we get"`
`∴" Area of the shaded region"=3.9375xx222/7`
`∴" Area of the shaded region"=12.375`
Therefore, area of the shaded region is`12.375 cm^2`
Now we will find the cost of painting the shaded region at the rate of 25 paise per cm2.
`∴ "Cost" =12.375xx25`
`∴ "Cost"=309.375` paise
`∴ "Cost"=Rs=3`
Therefore, cost of painting the shaded region to the nearest rupee is Rs `3`
APPEARS IN
संबंधित प्रश्न
A circular field has a perimeter of 650 m. A square plot having its vertices on the circumference of the field is marked in the field. Calculate the area of the square plot.
In the following figure, ABC is an equilateral triangle of side 8 cm. A, B and C are the centres of circular arcs of radius 4 cm. Find the area of the shaded region correct upto 2 decimal places. (Take π =3.142 and`sqrt3` = 1.732).

If the difference between the circumference and radius of a circle is 37 cm, then using π = \[\frac{22}{7}\] the circumference (in cm) of the circle is
ABCD is a rectangle whose three vertices are B (4,0), C (4,3) and D (0, 3). The length of one of its diagonals is
A wire is bent to form a square enclosing an area of 484 cm2. Using the same wire, a circle is formed. Find the area of the circle.
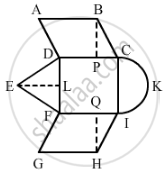
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
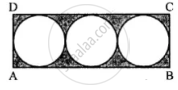
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
The length of the minute hand of a clock is 14 cm. The area swept by the minute hand in 5 minutes is ______.
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
