Advertisements
Advertisements
प्रश्न
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
विकल्प
31 cm
25 cm
62 cm
50 cm
उत्तर
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is 50 cm.
Explanation:
Let r1 = 24 cm and r2 = 7 cm
∴ Area of first circle = `π"r"_1^2`
= π(24)2
= 576π cm2
And area of second circle = `π"r"_2^2`
= π(7)2
= 49π cm2
According to the given condition,
Area of circle = Area of first circle + Area of second circle
∴ πR2 = 576π + 49π ...[Where, R be radius of circle]
⇒ R2 = 625
⇒ R = 25 cm
∴ Diameter of a circle = 2R
= 2 × 25
= 50 cm
APPEARS IN
संबंधित प्रश्न
The length and breadth of a rectangular garden are in the ratio 9:5. A path 3.5 m wide, running all around inside it has an area of `1911m^2` . Find the dimensions of the garden.
A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
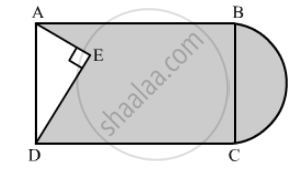
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
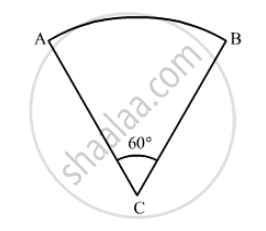
If the adjoining figure is a sector of a circle of radius 10.5 cm, what is the perimeter of the sector? (Take \[\pi = 22/7\])
If the perimeter of a sector of a circle of radius 6.5 cm is 29 cm, then its area is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
If diameter of a circle is increased by 40%, then its area increase by
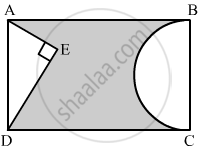
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

The circumference of a circular park is 352 m. Find the area of the park
