Advertisements
Advertisements
प्रश्न
The length and breadth of a rectangular garden are in the ratio 9:5. A path 3.5 m wide, running all around inside it has an area of `1911m^2` . Find the dimensions of the garden.
उत्तर
Let the length and breadth of the garden be 9x m and 5x m, respectively, Now,
Area of the garden=`(9x xx 5x)45x^2`
Length of the garden excluding the path =`(9x-7)`
Breadth of the garden excluding the path =`(5x-7)`
Area of the path = `45x^2=[(9x-7)(5x-7)]`
⇒ `1911=45x^2-[45x^2-63x-35x+49]`
⇒`1911=45x^2-45x^2+63x+35x-49`
⇒`1911=98x-49`
⇒`1960=98x`
⇒`x=1960/98`
⇒ `x=20`
Thus, we have:
Length=`9x=20xx9=180m`
Breadth=`5x=5xx20=100m`
APPEARS IN
संबंधित प्रश्न
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

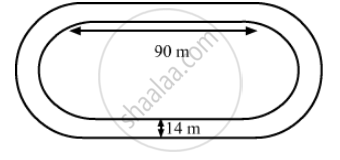
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
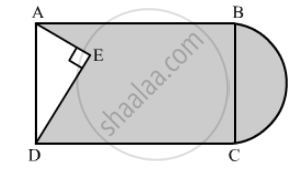
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
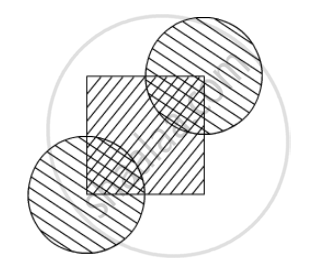
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
In a circle of radius 10 cm, an arc subtends an angle of 108° at the centre. what is the area of the sector in terms of π?
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
In the following figure, If ABC is an equilateral triangle, then shaded area is equal to
In the given figure, ABCD is a square each of whose sides measures 28 cm. Find the area of the shaded region.

The following figure shows two circles with the same center. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm.

Find:
(a) the area of the larger circle
(b) the area of the smaller circle
(c) the shaded area between the two circles. (π = 3.14)
The length of the minute hand of a clock is 14 cm. The area swept by the minute hand in 5 minutes is ______.
