Advertisements
Advertisements
प्रश्न
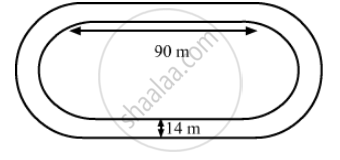
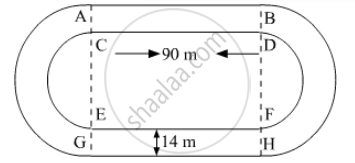
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
उत्तर
It is given that, `"length of each straight portion"`and `"width of track=14m"`
We know that the circumference C of semicircle of radius be r is \[C = \pi r\]
The inside perimeter of running track is the sum of twice the length of straight portion and circumferences of semicircles. So,
inside perimeter of running track = 400 m
\[2l + 2\pi r = 400 m\]
\[\Rightarrow 2 \times 90 + 2 \times \frac{22}{7} \times r = 400 m\]
\[\Rightarrow 2 \times 90 + 2 \times \frac{22}{7} \times r = 400 m\]
Thus, radius of inner semicircle is 35 m.
Now,
radius of outer semi circle r' = 35 + 14 = 49 m
Area of running track =\[2 \times \text{ Area of rectangle } + 2 \times \text{ Area of outer semi circle } - 2 \times \text{ Area of inner semicircle }\]
\[= 2 \times 90 \times 14 + 2 \times \frac{\pi(49 )^2}{2} - 2 \times \frac{\pi(35 )^2}{2}\]
\[= 2520 + \pi \times \left( 49 + 35 \right)\left( 49 - 35 \right)\]
\[= 2520 + \pi \times \left( 49 + 35 \right)\left( 49 - 35 \right)\]
\[= 2520 + 3696 = 6216 m^2\]
Hence, the area of running track = 6216 m2
Now, length L of outer running track isL = 2 × l + 2 \[\pi\]
\[= 2 \times 90 + 2\pi \times 49\]
\[= 180 + 2 \times \frac{22}{7} \times 49\]
\[= 180 + 308 = 488 m\]
Hence, the length L of outer running track is 488 m.
APPEARS IN
संबंधित प्रश्न
The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigating the park.
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then \[r_1^2 + r_2^2\]
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
The radii of two circles are 8 cm and 6 cm. Find the radius of the circle having area equal to the sum of the areas of the two circles.
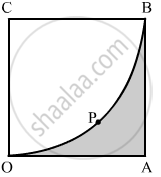
In the given figure, OABC is a square of side 7 cm. If COPB is a quadrant of a circle with centre C find the area of the shaded region.
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
The area of a circle is 1386 sq.cm; find its circumference.
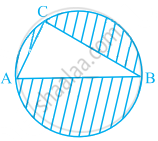
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).