Advertisements
Advertisements
प्रश्न
A rectangular park is 100 m by 50 m. It is surrounding by semi-circular flower beds all round. Find the cost of levelling the semi-circular flower beds at 60 paise per square metre (use π = 3.14).
उत्तर
Since four semicircular flower beds rounds the rectangular park. Then, diameters of semicircular plots are `2r_1=l and 2r_2=w`
`r_1=l/2`
`=100/2`
`=50 m`
Area of semicircular plot at larger side of rectangle`=1/2 pir^2`
`=1/2xx3.14xx50xx50`
`= 3925 m^2`
And the radius of semicircle at smaller side of rectangle
`r_2=l/2`
`=50/2`
`=25m`
Area of semicircluar plot at smaller side of rectangle=`1/2 pi r^2`
`=1/2xx3.14xx25xx25`
`=981.25 m^2`
Now, the total area of semicircular plot is sum of area of four semicircular plots.
Total Area of plot`=2xx3925+2xx981.25`
`=7850+192.5m^2`
`= 9812.5 m^2`
Since, The cost of levelling semicircular flower bed per square meter=` Rs 0.60`
So, The cost of levelling 9812.5 square meter flower bed= `Rs0.60xx9812.5`
=` Rs 5887.50`
APPEARS IN
संबंधित प्रश्न
A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
In the given figure ABCD is quadrilateral in which diagonal BD = 24 cm, AL ⊥ BD and CM ⊥ BD such that AL = 9cm and CM = 12 cm. Calculate the area of the quadrilateral.
The outer circumference of a circular race-track is 528 m . The track is everywhere 14 m wide. Calculate the cost of levelling the track at the rate of 50 paise per square metre.
`(use pi=22/7). `
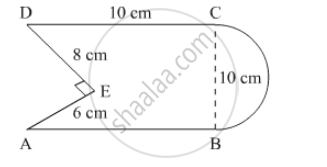
Find the area of the following figure, in square cm, correct to one place of decimal. (Take π = 22/7).
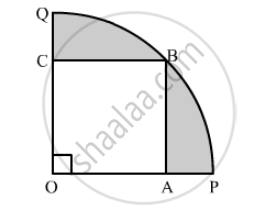
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then \[r_1^2 + r_2^2\]
Find the lengths of the arcs cut off from a circle of radius 12 cm by a chord 12 cm long. Also, find the area of the minor segment.
The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
