Advertisements
Advertisements
प्रश्न
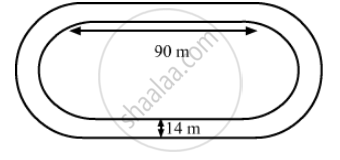
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
उत्तर
It is given that, `"length of each straight portion"`and `"width of track=14m"`
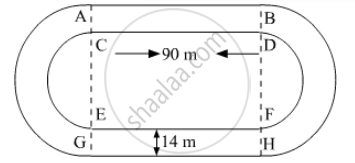
We know that the circumference C of semicircle of radius be r is \[C = \pi r\]
The inside perimeter of running track is the sum of twice the length of straight portion and circumferences of semicircles. So,
inside perimeter of running track = 400 m
\[2l + 2\pi r = 400 m\]
\[\Rightarrow 2 \times 90 + 2 \times \frac{22}{7} \times r = 400 m\]
\[\Rightarrow 2 \times 90 + 2 \times \frac{22}{7} \times r = 400 m\]
Thus, radius of inner semicircle is 35 m.
Now,
radius of outer semi circle r' = 35 + 14 = 49 m
Area of running track =\[2 \times \text{ Area of rectangle } + 2 \times \text{ Area of outer semi circle } - 2 \times \text{ Area of inner semicircle }\]
\[= 2 \times 90 \times 14 + 2 \times \frac{\pi(49 )^2}{2} - 2 \times \frac{\pi(35 )^2}{2}\]
\[= 2520 + \pi \times \left( 49 + 35 \right)\left( 49 - 35 \right)\]
\[= 2520 + \pi \times \left( 49 + 35 \right)\left( 49 - 35 \right)\]
\[= 2520 + 3696 = 6216 m^2\]
Hence, the area of running track = 6216 m2
Now, length L of outer running track isL = 2 × l + 2 \[\pi\]
\[= 2 \times 90 + 2\pi \times 49\]
\[= 180 + 2 \times \frac{22}{7} \times 49\]
\[= 180 + 308 = 488 m\]
Hence, the length L of outer running track is 488 m.
APPEARS IN
संबंधित प्रश्न
The length of a rectangular park is twice its breadth and its perimeter is 840 m. Find the area of the park.
A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
The outer circumference of a circular race-track is 528 m . The track is everywhere 14 m wide. Calculate the cost of levelling the track at the rate of 50 paise per square metre.
`(use pi=22/7). `
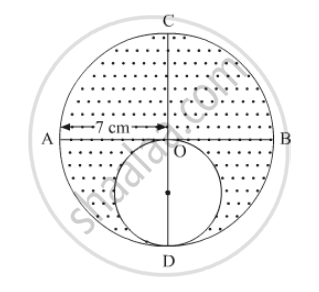
In the following figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
The circumference of a circle is 100 m. The side of a square inscribed in the circle is
If a chord of a circle of radius 28 cm makes an angle of 90 ° at the centre, then the area of the major segment is
A wire is bent to form a square enclosing an area of 484 cm2. Using the same wire, a circle is formed. Find the area of the circle.
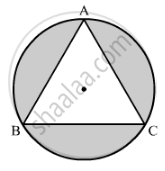
On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. `["Use" sqrt(3) = 1.73, pi =22/7]`
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be ______.
