Advertisements
Advertisements
प्रश्न
On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. `["Use" sqrt(3) = 1.73, pi =22/7]`
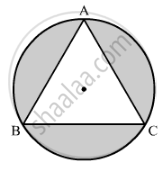
उत्तर
Construction: Join AO and extend it to D on BC.
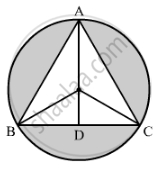
Radius of the circle, r = 42 cm
∠OCD= 30°
cos30° `= "DC"/"OC"`
`=> sqrt(3)/2 = "DC"/42`
`⇒ "DC" = 21sqrt(3)`
`=> "DC" = 2xx"DC" = 42sqrt(3) = 72.66 "cm"`
sin 30°`="OD"/"OC"`
`=> 1/2="OD"/42`
⇒ OD = 21 cm
Now, AD = AO + OD = 42 + 21 = 63 cm
Area of shaded region = Area of circlec - Area of triangle ABC
`= pi(OA)^2-1/2xx"AD"xx"AB"`
`=22/7(42)^2-1/2xx63xx72.66`
= 5544 - 2288.79
= 3255.21 cm2
APPEARS IN
संबंधित प्रश्न
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
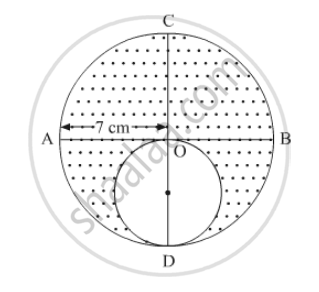
In the following figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
The length of an arc of a circle, subtending an angle of 54° at the centre, is 16.5 cm. Calculate the radius, circumference and area of the circle.
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
The length of the minute hand of a clock is 21 cm. The area swept by the minute hand in 10 minutes is
The given figures show a rectangle ABCD inscribed in a circle as shown alongside.
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.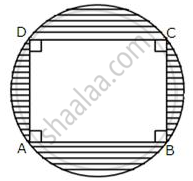
Find the area of a flat circular ring formed by two concentric circles (circles with the same centre) whose radii are 9 cm and 5 cm.
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
Perimeter of a sector of a circle whose central angle is 90° and radius 7 cm is ____________.
