Advertisements
Advertisements
प्रश्न
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use `sqrt(3)= 1.73, pi = 3.14]`
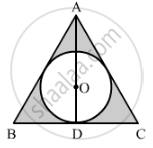
उत्तर
We can find the radius of the incircle by using the formula
`"r" = 2xx"Area of triangle"/"Perimeter of triangle" = (2xxsqrt(3)/4xx(12)^2)/(3xx12) = 2sqrt(3) "cm"`
Now, area of shaded region = Area of triangle - Area of circle
`= sqrt(3)/4xx(12)^2-3.14xx(2sqrt(3))^2`
=62.28-37.68
= 24.6 cm2
Hence, the area of shaded region is 24.6 cm2
APPEARS IN
संबंधित प्रश्न
The cost of painting the four walls of a room 12 m long at `₹ 30 per m^2 is ₹ 7560 per m^2` and the cost of covering the floor with the mat at ₹` 25 per m^2 is ₹ 2700 `. find the dimensions of the room.
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
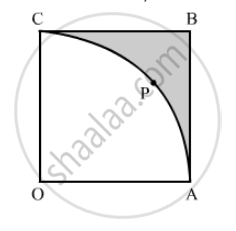
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
If diameter of a circle is increased by 40%, then its area increase by
The length of an arc of the sector of angle θ° of a circle with radius R is
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area the circle.
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
Find the area enclosed between two concentric circles, If their radii are 6cm and 13cm respectively.
Diameter of a circular garden is 9.8 m. Find its area.
