Advertisements
Advertisements
प्रश्न
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
उत्तर
In a circle
Circumference = Sum of circumferences of two circle of radii 15 cm and 13 cm
Now circumference of first smaller circle = 2πr
= `2 xx 22/7 xx 15 = 660/7` cm
Circumference of the second smaller circle
= `2 xx 22/7 xx 13 = 572/7` cm
∴ Circumference of the bigger circle
= `660/7 + 572/7 = 1232/7` cm
Let R be its radius, then
`2pi"R" = 1232/7 ⇒ (2 xx 22)/7 "R" = 1232/7`
⇒ R = `1232/7 xx 7/44 = 28` cm
∴ Area of the circle = `pi"R"^2`
= `22/7 xx 28 xx 28 "cm"^2 = 2464` cm2
APPEARS IN
संबंधित प्रश्न
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of the sector of the circle formed by chord AB.
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
In a circle of radius 10 cm, an arc subtends an angle of 108° at the centre. what is the area of the sector in terms of π?
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
The area of a circle is 220 cm2. The area of ta square inscribed in it is
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
The cost of fencing a circular field at the rate of Rs 25 per metre is Rs 5500. The field is to be ploughed at the rate of 50 paise per m2 . Find the cost of ploughing the field. [Take `π =22/7`].
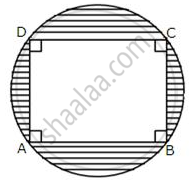
The given figures show a rectangle ABCD inscribed in a circle as shown alongside.
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.