Advertisements
Online Mock Tests
Chapters
2: Exponents
3: Squares and Square Root
4: Cubes and Cube Roots
5: Playing with Numbers
6: Sets
7: Percent and Percentage
8: Profit, Loss and Discount
9: Interest
10: Direct and Inverse Variations
11: Algebraic Expressions
12: Identities
13: Factorisation
14: Linear Equations in one Variable
15: Linear Inequations
16: Understanding Shapes
17: Special Types of Quadrilaterals
18: Constructions
19: Representing 3-D in 2-D
▶ 20: Area of a Trapezium and a Polygon
21: Surface Area, Volume and Capacity
22: Data Handling
23: Probability
![Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 20 - Area of a Trapezium and a Polygon Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 20 - Area of a Trapezium and a Polygon - Shaalaa.com](/images/concise-mathematics-english-class-8-icse_6:3b78c4422443458583dde48f228ef792.jpg)
Advertisements
Solutions for Chapter 20: Area of a Trapezium and a Polygon
Below listed, you can find solutions for Chapter 20 of CISCE Selina for Concise Mathematics [English] Class 8 ICSE.
Selina solutions for Concise Mathematics [English] Class 8 ICSE 20 Area of a Trapezium and a Polygon Exercise 20 (A) [Pages 223 - 224]
Find the area of a triangle, whose sides are :
10 cm, 24 cm, and 26 cm
Find the area of a triangle, whose sides are :
18 mm, 24 mm and 30 mm
Find the area of a triangle, whose sides are :
21 m, 28 m, and 35 m
Two sides of a triangle are 6 cm and 8 cm. If the height of the triangle corresponding to 6 cm side is 4 cm; find :
(i) area of the triangle
(ii) height of the triangle corresponding to 8 cm side.
The sides of a triangle are 16 cm, 12 cm, and 20 cm. Find :
(i) area of the triangle ;
(ii) height of the triangle, corresponding to the largest side ;
(iii) height of the triangle, corresponding to the smallest side.
Two sides of a triangle are 6.4 m and 4.8 m. If the height of the triangle corresponding to 4.8 m side is 6 m;
find :
(i) area of the triangle ;
(ii) height of the triangle corresponding to 6.4 m sides.
The base and the height of a triangle are in the ratio 4: 5. If the area of the triangle is 40 m2; find its base and height.
The base and the height of a triangle are in the ratio 5 : 3. If the area of the triangle is 67.5 m2; find its base and height.
The area of an equilateral triangle is `144sqrt3` cm2; find its perimeter.
The area of an equilateral triangle is numerically equal to its perimeter. Find its perimeter correct to 2 decimal places.
A field is in the shape of a quadrilateral ABCD in which side AB = 18 m, side AD = 24 m, side BC = 40m, DC = 50 m and angle A = 90°. Find the area of the field.
The lengths of the sides of a triangle are in the ratio 4: 5 : 3 and its perimeter is 96 cm. Find its area.
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
The altitude and the base of a triangular field are in the ratio 6: 5. If its cost is ₹ 49,57,200 at the rate of ₹ 36,720 per hectare and 1 hectare = 10,000 sq. m, find (in metre) dimensions of the field.
Find the area of the right-angled triangle with a hypotenuse of 40 cm and one of the other two sides of 24 cm.
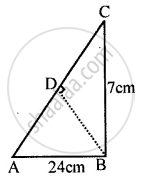
Use the information given in the adjoining figure to find :
(i) the length of AC.
(ii) the area of an ∆ABC
(iii) the length of BD, correct to one decimal place.
Selina solutions for Concise Mathematics [English] Class 8 ICSE 20 Area of a Trapezium and a Polygon Exercise 20 (B) [Pages 227 - 228]
Find the length and perimeter of a rectangle, whose area = 120 cm2 and breadth = 8 cm
The perimeter of a rectangle is 46 m and its length is 15 m. Find its :
(i) breadth
(ii) area
(iii) diagonal.
The diagonal of a rectangle is 34 cm. If its breadth is 16 cm; find its :
(i) length
(ii) area
The area of a small rectangular plot is 84 m2. If the difference between its length and the breadth is 5 m; find its perimeter.
The perimeter of a square is 36 cm; find its area
Find the perimeter of a square; whose area is: 1.69 m2
The diagonal of a square is 12 cm long; find its area and length of one side.
The diagonal of a square is 15 m; find the length of its one side and perimeter.
The area of a square is 169 cm2. Find its:
(i) one side
(ii) perimeter
The length of a rectangle is 16 cm and its perimeter is equal to the perimeter of a square with side 12.5 cm. Find the area of the rectangle.
The perimeter of a square is numerically equal to its area. Find its area.
Each side of a rectangle is doubled. Find the ratio between :
(i) perimeters of the original rectangle and the resulting rectangle.
(ii) areas of the original rectangle and the resulting rectangle.
In each of the following cases, ABCD is a square and PQRS is a rectangle. Find, in each case, the area of the shaded portion.
(All measurements are in metre).
(i)
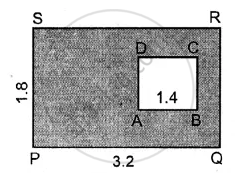
(ii)
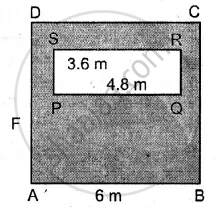
A path of uniform width, 3 m, runs around the outside of a square field of side 21 m. Find the area of the path.
A path of uniform width, 2.5 m, runs around the inside of a rectangular field 30 m by 27 m. Find the area of the path.
The length of a hall is 18 m and its width is 13.5 m. Find the least number of square tiles, each of side 25 cm, required to cover the floor of the hall,
(i) without leaving any margin.
(ii) leaving a margin of width 1.5 m all around. In each case, find the cost of the tiles required at the rate of Rs. 6 per tile
A rectangular field is 30 m in length and 22m in width. Two mutually perpendicular roads, each 2.5 m wide, are drawn inside the field so that one road is parallel to the length of the field and the other road is parallel to its width. Calculate the area of the crossroads.
The length and the breadth of a rectangular field are in the ratio 5: 4 and its area is 3380 m2. Find the cost of fencing it at the rate of ₹75 per m.
The length and the breadth of a conference hall are in the ratio 7: 4 and its perimeter is 110 m. Find:
(i) area of the floor of the hall.
(ii) a number of tiles, each a rectangle of size 25 cm x 20 cm, required for the flooring of the hall.
(iii) the cost of the tiles at the rate of ₹ 1,400 per hundred tiles.
Selina solutions for Concise Mathematics [English] Class 8 ICSE 20 Area of a Trapezium and a Polygon Exercise 20 (C) [Page 232]
The following figure shows the cross-section ABCD of a swimming pool which is a trapezium in shape.
If the width DC, of the swimming pool, is 6.4 m, depth (AD) at the shallow end is 80 cm and depth (BC) at the deepest end is 2.4 m, find its area of the cross-section.
The parallel sides of a trapezium are in ratio 3: 4. If the distance between the parallel sides is 9 dm and its area is 126 dm2; find the lengths of its parallel sides.
The two parallel sides and the distance between them are in the ratio 3: 4: 2. If the area of the trapezium is 175 cm2, find its height.
A parallelogram has sides of 15 cm and 12 cm; if the distance between the 15 cm sides is 6 cm; find the distance between 12 cm sides.
A parallelogram has sides of 20 cm and 30 cm. If the distance between its shorter sides is 15 cm; find the distance between the longer sides.
The adjacent sides of a parallelogram are 21 cm and 28 cm. If it's one diagonal is 35 cm; find the area of the parallelogram.
The diagonals of a rhombus are 18 cm and 24 cm. Find:
(i) its area ;
(ii) length of its sides.
(iii) its perimeter
The perimeter of a rhombus is 40 cm. If one diagonal is 16 cm; find:
- It's other diagonal
- area
Each side of a rhombus is 18 cm. If the distance between two parallel sides is 12 cm, find its area.
The length of the diagonals of a rhombus is in ratio 4 : 3. If its area is 384 cm2, find its side.
A thin metal iron-sheet is rhombus in shape, with each side 10 m. If one of its diagonals is 16 m, find the cost of painting both sides at the rate of ₹ 6 per m2. Also, find the distance between the opposite sides of this rhombus.
The area of a trapezium is 279 sq.cm and the distance between its two parallel sides is 18 cm. If one of its parallel sides is longer than the other side by 5 cm, find the lengths of its parallel sides.
The area of a rhombus is equal to the area of a triangle. If the base ∆ is 24 cm, its corresponding altitude is 16 cm and one of the diagonals of the rhombus is 19.2 cm. Find its other diagonal.
Find the area of the trapezium ABCD in which AB || DC, AB = 18 cm, ∠B = ∠C = 90°, CD = 12 cm and AD = 10 cm.
Selina solutions for Concise Mathematics [English] Class 8 ICSE 20 Area of a Trapezium and a Polygon Exercise 20 (D) [Pages 234 - 235]
Find the radius and area of a circle, whose circumference is :
(i) 132 cm
(ii) 22 m
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
The circumference of a circular table is 88 m. Find its area.
The area of a circle is 1386 sq.cm; find its circumference.
Find the area of a flat circular ring formed by two concentric circles (circles with the same centre) whose radii are 9 cm and 5 cm.
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
There is a path of uniform width 7 m round and outside a circular garden of diameter 210 m. Find the area of the path.
A wire, when bent in the form of a square encloses an area of 484 cm2. Find :
(i) one side of the square ;
(ii) length of the wire ;
(iii) the largest area enclosed; if the same wire is bent to form a circle.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
The radius of a circular wheel is 42 cm. Find the distance travelled by it in :
(i) 1 revolution ;
(ii) 50 revolutions ;
(iii) 200 revolutions ;
The diameter of a wheel is 0.70 m. Find the distance covered by it in 500 revolutions. If the wheel takes 5 minutes to make 500 revolutions; find its speed in :
(i) m/s
(ii) km/hr.
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
A piece of wire of length 108 cm is bent to form a semicircular arc bounded by its diameter. Find its radius and area enclosed.
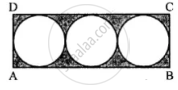
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
Solutions for 20: Area of a Trapezium and a Polygon
![Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 20 - Area of a Trapezium and a Polygon Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 20 - Area of a Trapezium and a Polygon - Shaalaa.com](/images/concise-mathematics-english-class-8-icse_6:3b78c4422443458583dde48f228ef792.jpg)
Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 20 - Area of a Trapezium and a Polygon
Shaalaa.com has the CISCE Mathematics Concise Mathematics [English] Class 8 ICSE CISCE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Selina solutions for Mathematics Concise Mathematics [English] Class 8 ICSE CISCE 20 (Area of a Trapezium and a Polygon) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Selina textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Concise Mathematics [English] Class 8 ICSE chapter 20 Area of a Trapezium and a Polygon are Perimeter of Triangles, Perimeter of Squares, Area of a Parallelogram, Area of a Rhombus, Area of Circle, Area of Trapezium, Perimeter of a Rectangle.
Using Selina Concise Mathematics [English] Class 8 ICSE solutions Area of a Trapezium and a Polygon exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Selina Solutions are essential questions that can be asked in the final exam. Maximum CISCE Concise Mathematics [English] Class 8 ICSE students prefer Selina Textbook Solutions to score more in exams.
Get the free view of Chapter 20, Area of a Trapezium and a Polygon Concise Mathematics [English] Class 8 ICSE additional questions for Mathematics Concise Mathematics [English] Class 8 ICSE CISCE, and you can use Shaalaa.com to keep it handy for your exam preparation.
