Advertisements
Advertisements
प्रश्न
The area of an equilateral triangle is `144sqrt3` cm2; find its perimeter.
उत्तर
Let each side of an equilateral triangle = x cm
∴ Its area = `sqrt(3)/4 ("side")^2`
= `sqrt(3)/4 x^2 = 144sqrt(3)` (given)
⇒ `x^2 = 144sqrt(3) xx 4/sqrt(3)`
⇒ `x^2 = 144 xx 4 ⇒ x^2 = 576`
⇒ x = `sqrt(576)` = 24 cm.
⇒ Each side = 24 cm
Hence perimeter = 3(24) = 72 cm.
APPEARS IN
संबंधित प्रश्न
Find the area of an isosceles triangle with perimeter is 36 cm and the base is 16 cm.
The perimeter of a triangle is 450 m and its side are in the ratio 12: 5: 13. Find the area of the triangle.
The base and the height of a triangle are in the ratio 4: 5. If the area of the triangle is 40 m2; find its base and height.
The base and the height of a triangle are in the ratio 5 : 3. If the area of the triangle is 67.5 m2; find its base and height.
The area of an equilateral triangle is numerically equal to its perimeter. Find its perimeter correct to 2 decimal places.
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
The altitude and the base of a triangular field are in the ratio 6: 5. If its cost is ₹ 49,57,200 at the rate of ₹ 36,720 per hectare and 1 hectare = 10,000 sq. m, find (in metre) dimensions of the field.
The base of a triangle field and its height are in the ratio 2:5. If the cost of cultivating the field at Rs.42 per sq. m is Rs.7560, find its base and height.
The cost of fencing a triangular field at the rate of Rs.15 per m is Rs.900. If the lengths of the triangle are in the ratio 3:4:5, find the area of the triangle and the cost of cultivating it at Rs.48 per kg sq.m.
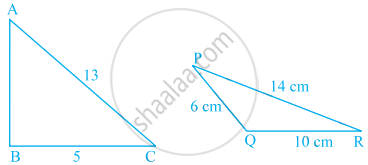
In the given figures, perimeter of ΔABC = perimeter of ΔPQR. Find the area of ΔABC.