Advertisements
Advertisements
प्रश्न
The cost of fencing a triangular field at the rate of Rs.15 per m is Rs.900. If the lengths of the triangle are in the ratio 3:4:5, find the area of the triangle and the cost of cultivating it at Rs.48 per kg sq.m.
Advertisements
उत्तर
Let the Perimeter of the triangular plot of land = P
∴ P x 15 = 900
⇒ P = `(900)/(15)`
= 60
Let the sides of the triangular plot of land = 3x, 4x and 5x
So,
3x + 4x + 5x
=60
⇒ x = 5
So, the sides of the triangular plot of land
= 3 x 5, 4x 5 and 5 x 5
= 15m, 20m, 25m
We know that, Area of a Triangle whose sides are a, B, and c and semiperimeter is s given by `sqrt("s"("s" - "a")("s" - "b")("s" - "c")) ; "s" = ("a" + "b" + "c")/(2)`
For a triangle whose sides are cm, cm and cm
ie a= 15 b = 20 and c = 25, s = `(60)/(2)` = 30
Area
= `sqrt(30(30 - 15)(30 - 15)(30 - 20)(30 - 25)`
= `sqrt(30(15)(10)(5)`
= `sqrt(22500)`
= 150cm2
Cost of cultivating 1m2 = Rs.48
Cost of cultivating 150m2
= Rs.48 x 150
= Rs.7200.
APPEARS IN
संबंधित प्रश्न
If the difference between the sides of a right-angled triangle is 3 cm and its area is 54 cm2; find its perimeter.
In triangle ABC; angle A = 90o, side AB = x cm, AC = (x + 5) cm and area = 150 cm2. Find the sides of the triangle.
Find the area of a triangle, whose sides are :
18 mm, 24 mm and 30 mm
Two sides of a triangle are 6 cm and 8 cm. If the height of the triangle corresponding to 6 cm side is 4 cm; find :
(i) area of the triangle
(ii) height of the triangle corresponding to 8 cm side.
Two sides of a triangle are 6.4 m and 4.8 m. If the height of the triangle corresponding to 4.8 m side is 6 m;
find :
(i) area of the triangle ;
(ii) height of the triangle corresponding to 6.4 m sides.
The base of a triangle field and its height are in the ratio 2:5. If the cost of cultivating the field at Rs.42 per sq. m is Rs.7560, find its base and height.
The table given below contains some measures of the triangle. Find the unknown values.
| Side 1 | Side 2 | Side 3 | Perimeter |
| 6 cm | 5 cm | 2 cm | ? |
Find the perimeter of An equilateral triangle with side 6 cm
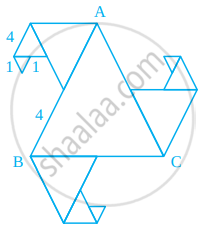
In the following figure, all triangles are equilateral and AB = 8 units. Other triangles have been formed by taking the mid points of the sides. What is the perimeter of the figure?
Area of an isosceles triangle is 48 cm2. If the altitudes corresponding to the base of the triangle is 8 cm, find the perimeter of the triangle.
