Advertisements
Advertisements
प्रश्न
The area of an equilateral triangle is numerically equal to its perimeter. Find its perimeter correct to 2 decimal places.
उत्तर १
Let each side of the equilateral triangle = x
∴ Its area = `sqrt(3)/4 x^2`
Area perimeter = 3x
By the given condition = `sqrt(3)/4 x^2 = 3x`
`x^2 = 3x xx 4/sqrt(3)`
`x^2 = (3x xx 4 xx sqrt(3))/(sqrt(3) xx sqrt(3)) = (3x xx 4 xx sqrt(3))/3 = 4xsqrt(3)`
⇒ `x^2 = sqrt(3) (4x) ⇒ x = 4sqrt(3)` [∵ x ≠ 0]
∴ Perimeter = `12sqrt(3)` units
= 12 (1.732) = 20.784 = 20.78 units
उत्तर २
Let the side length of the equilateral triangle be a.
Step 1: Write the formula for the area and the perimeter
- Area of an equilateral triangle: Area = `sqrt3/4 a^2`
- Perimeter of the triangle: Perimeter = 3a
Step 2: Given that the area equals the perimeter
`sqrt3/4 a^2 = 3a`
Step 3: Simplify the equation
Divide through by a (assuming a ≠ 0): `sqrt3/4 a = 3`
Multiply through by 4: `sqrt3 a = 12`
Divide by `sqrt3`: `a = 12/sqrt3`
Rationalize the denominator: `a = (12sqrt3)/3 = 4sqrt3`
Step 4: Calculate the perimeter
Perimeter = 3a
`= 3(4sqrt3) = 12sqrt3`
Step 5: Approximate to 2 decimal places
Using `sqrt3 = 1.732`
12√3 = 12 × 1.732 = 20.784
= 20.784
APPEARS IN
संबंधित प्रश्न
The length of the sides of a triangle are in the ratio 3: 4: 5. Find the area of the triangle if its perimeter is 144 cm.
The sides of a triangular field are in the ratio 5: 3: 4 and its perimeter is 180 m. Find:
(i) its area.
(ii) the altitude of the triangle corresponding to its largest side.
(iii) the cost of leveling the field at the rate of Rs. 10 per square meter.
The perimeter of a triangle is 450 m and its side are in the ratio 12: 5: 13. Find the area of the triangle.
The base and the height of a triangle are in the ratio 4: 5. If the area of the triangle is 40 m2; find its base and height.
A field is in the shape of a quadrilateral ABCD in which side AB = 18 m, side AD = 24 m, side BC = 40m, DC = 50 m and angle A = 90°. Find the area of the field.
The lengths of the sides of a triangle are in the ratio 4: 5 : 3 and its perimeter is 96 cm. Find its area.
Find the area of a triangle whose sides are in the ratio 5:12:13 and whose perimeter is 36cm.
The table given below contains some measures of the triangle. Find the unknown values.
| Side 1 | Side 2 | Side 3 | Perimeter |
| ? | 8 m | 3 m | 17 m |
The scalene triangle has 40 cm as its perimeter and whose two sides are 13 cm and 15 cm, find the third side
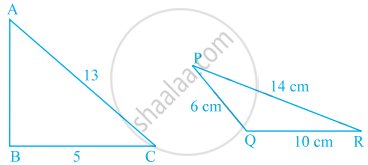
In the given figures, perimeter of ΔABC = perimeter of ΔPQR. Find the area of ΔABC.