Advertisements
Advertisements
प्रश्न
The length of the sides of a triangle are in the ratio 3: 4: 5. Find the area of the triangle if its perimeter is 144 cm.
उत्तर
Let the sides of the triangle are
a = 3x
b = 4x
c = 5x
Given that the perimeter is 144 cm.
Hence
3x + 4x + 5x = 144
⇒ 12x = 144
⇒ x = `144/12`
⇒ x = 12
s = `(a + b + c)/(2)`
= `(12x)/(2)`
= 6x
= 6 × 12
= 72
The sides are a = 36 cm, b = 48 cm and c = 60 cm.
Area of the triangle is
A = `sqrt (s(s - a )( s - b ) (s - c ))`
= `sqrt (72(72 - 36 )( 72 - 48 ) (72 - 60))`
= `sqrt (72 xx 36 xx 24 xx 12)`
= `sqrt746496`
= 864 cm2
APPEARS IN
संबंधित प्रश्न
Find the area of a triangle, whose sides are :
10 cm, 24 cm, and 26 cm
Find the area of a triangle, whose sides are :
18 mm, 24 mm and 30 mm
The area of an equilateral triangle is numerically equal to its perimeter. Find its perimeter correct to 2 decimal places.
The lengths of the sides of a triangle are in the ratio 4: 5 : 3 and its perimeter is 96 cm. Find its area.
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
The altitude and the base of a triangular field are in the ratio 6: 5. If its cost is ₹ 49,57,200 at the rate of ₹ 36,720 per hectare and 1 hectare = 10,000 sq. m, find (in metre) dimensions of the field.
Find the area of the right-angled triangle with a hypotenuse of 40 cm and one of the other two sides of 24 cm.
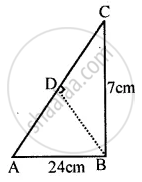
Use the information given in the adjoining figure to find :
(i) the length of AC.
(ii) the area of an ∆ABC
(iii) the length of BD, correct to one decimal place.
Find the area of a triangle with a base 12cm and a height equal to the width of a rectangle having area of 96cm2 and a length of 12cm.
The table given below contains some measures of the triangle. Find the unknown values.
| Side 1 | Side 2 | Side 3 | Perimeter |
| ? | 8 m | 3 m | 17 m |
