Advertisements
Advertisements
Question
The length of the sides of a triangle are in the ratio 3: 4: 5. Find the area of the triangle if its perimeter is 144 cm.
Solution
Let the sides of the triangle are
a = 3x
b = 4x
c = 5x
Given that the perimeter is 144 cm.
Hence
3x + 4x + 5x = 144
⇒ 12x = 144
⇒ x = `144/12`
⇒ x = 12
s = `(a + b + c)/(2)`
= `(12x)/(2)`
= 6x
= 6 × 12
= 72
The sides are a = 36 cm, b = 48 cm and c = 60 cm.
Area of the triangle is
A = `sqrt (s(s - a )( s - b ) (s - c ))`
= `sqrt (72(72 - 36 )( 72 - 48 ) (72 - 60))`
= `sqrt (72 xx 36 xx 24 xx 12)`
= `sqrt746496`
= 864 cm2
APPEARS IN
RELATED QUESTIONS
If the difference between the sides of a right-angled triangle is 3 cm and its area is 54 cm2; find its perimeter.
In triangle ABC; angle A = 90o, side AB = x cm, AC = (x + 5) cm and area = 150 cm2. Find the sides of the triangle.
The base of a triangular field is three times its height. If the cost of cultivating the field at ₹ 36.72 per 100 m2 is ₹ 49,572; find its base and height.
Find the area of a triangle, whose sides are :
18 mm, 24 mm and 30 mm
Two sides of a triangle are 6.4 m and 4.8 m. If the height of the triangle corresponding to 4.8 m side is 6 m;
find :
(i) area of the triangle ;
(ii) height of the triangle corresponding to 6.4 m sides.
The lengths of the sides of a triangle are in the ratio 4: 5 : 3 and its perimeter is 96 cm. Find its area.
The perimeter of a triangle is 72cm and its sides are in the ratio 3:4:5. Find its area and the length of the altitude corresponding to the longest side.
Find the perimeter and the area of a right angled triangle whose sides are 6 feet, 8 feet and 10 feet
In the given figure, all triangles are equilateral and AB = 8 units. Other triangles have been formed by taking the mid points of the sides. What is the perimeter of the figure?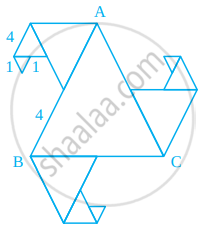
Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
