Advertisements
Advertisements
Question
Find the area of a triangle whose sides are 18 cm, 24 cm, and 30 cm. Also, find the length of altitude corresponding to the largest side of the triangle.
Solution
Since the sides of the triangle are 18 cm, 24 cm and 30 cm respectively.
s = `(18 + 24 + 30)/(2)`
= 36
Hence the area of the triangle is
A = `sqrt (s( s - a ) ( s - b ) (s -c ))`
= `sqrt (36( 36 - 18 ) ( 36 - 24 ) (36 -30 ))`
= `sqrt (36 xx 18 xx 12 xx 6 )`
= ` sqrt ( 46656 ) `
= 216 sq.cm.
Again
A = `1/2 "base" xx "altitude" `
Hence
216 = `1/2 xx 30 xx h`
h = 14.4cm
APPEARS IN
RELATED QUESTIONS
AD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that ∠BOC = 90o. Find the area of quadrilateral ABOC.
In triangle ABC; angle A = 90o, side AB = x cm, AC = (x + 5) cm and area = 150 cm2. Find the sides of the triangle.
Calculate the area and the height of an equilateral triangle whose perimeter is 60 cm.
The base of a triangular field is three times its height. If the cost of cultivating the field at ₹ 36.72 per 100 m2 is ₹ 49,572; find its base and height.
The area of an equilateral triangle is numerically equal to its perimeter. Find its perimeter correct to 2 decimal places.
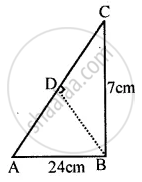
Use the information given in the adjoining figure to find :
(i) the length of AC.
(ii) the area of an ∆ABC
(iii) the length of BD, correct to one decimal place.
Find the area of a triangle with a base 12cm and a height equal to the width of a rectangle having area of 96cm2 and a length of 12cm.
Find the area of a triangle with a base 12cm and a height equal to the width of a rectangle having area of 96cm2 and a length of 12cm.
From one vertex of an equilateral triangle with side 40 cm, an equilateral triangle with 6 cm side is removed. What is the perimeter of the remaining portion?
Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
