Advertisements
Advertisements
प्रश्न
Find the area of a triangle whose sides are 18 cm, 24 cm, and 30 cm. Also, find the length of altitude corresponding to the largest side of the triangle.
उत्तर
Since the sides of the triangle are 18 cm, 24 cm and 30 cm respectively.
s = `(18 + 24 + 30)/(2)`
= 36
Hence the area of the triangle is
A = `sqrt (s( s - a ) ( s - b ) (s -c ))`
= `sqrt (36( 36 - 18 ) ( 36 - 24 ) (36 -30 ))`
= `sqrt (36 xx 18 xx 12 xx 6 )`
= ` sqrt ( 46656 ) `
= 216 sq.cm.
Again
A = `1/2 "base" xx "altitude" `
Hence
216 = `1/2 xx 30 xx h`
h = 14.4cm
APPEARS IN
संबंधित प्रश्न
Two sides of a triangle are 6 cm and 8 cm. If the height of the triangle corresponding to 6 cm side is 4 cm; find :
(i) area of the triangle
(ii) height of the triangle corresponding to 8 cm side.
The base and the height of a triangle are in the ratio 5 : 3. If the area of the triangle is 67.5 m2; find its base and height.
The area of an equilateral triangle is `144sqrt3` cm2; find its perimeter.
A field is in the shape of a quadrilateral ABCD in which side AB = 18 m, side AD = 24 m, side BC = 40m, DC = 50 m and angle A = 90°. Find the area of the field.
Find the area of the right-angled triangle with a hypotenuse of 40 cm and one of the other two sides of 24 cm.
Find the area of a triangle with a base 12cm and a height equal to the width of a rectangle having area of 96cm2 and a length of 12cm.
The table given below contains some measures of the triangle. Find the unknown values.
| Side 1 | Side 2 | Side 3 | Perimeter |
| 11 feet | ? | 9 feet | 28 feet |
The scalene triangle has 40 cm as its perimeter and whose two sides are 13 cm and 15 cm, find the third side
The perimeter of a triangle is 28 cm. One of it’s sides is 8cm. Write all the sides of the possible isosceles triangles with these measurements.
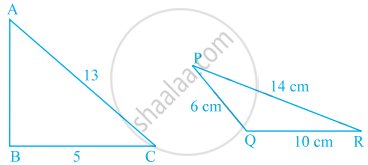
In the given figures, perimeter of ΔABC = perimeter of ΔPQR. Find the area of ΔABC.