Advertisements
Advertisements
प्रश्न
A field is in the shape of a quadrilateral ABCD in which side AB = 18 m, side AD = 24 m, side BC = 40m, DC = 50 m and angle A = 90°. Find the area of the field.
उत्तर
Since ∠A = 90°
By Pythagorus Theorem,
In ∆ABD,
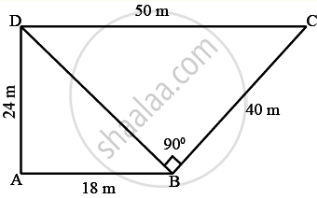
Now, the area of ΔABD = `1/2 (18)(24)`
= (18) (12) = 216 m2
In ΔABD
BD = `sqrt("AB"^2 + "AD"^2) = sqrt(18^2 + 24^2)`
= `sqrt(324 + 576) = sqrt(900) = 30`m.
S = `120/20 = 60 cm^2`
=`sqrt( 60xx10xx20xx30)`
= `sqrt(10xx2xx3xx10xx10xx2xx10xx3)`
= 10 × 10 × 6
= 600 cm2
Area of quadrilateral ABCD
= 816cm2
APPEARS IN
संबंधित प्रश्न
Find the area of a triangle whose sides are 18 cm, 24 cm, and 30 cm. Also, find the length of altitude corresponding to the largest side of the triangle.
AD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that ∠BOC = 90o. Find the area of quadrilateral ABOC.
The length of the sides of a triangle are in the ratio 3: 4: 5. Find the area of the triangle if its perimeter is 144 cm.
The base of a triangular field is three times its height. If the cost of cultivating the field at ₹ 36.72 per 100 m2 is ₹ 49,572; find its base and height.
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
Find the area of a triangle whose sides are in the ratio 5:12:13 and whose perimeter is 36cm.
The base of a triangle field and its height are in the ratio 2:5. If the cost of cultivating the field at Rs.42 per sq. m is Rs.7560, find its base and height.
The cost of fencing a triangular field at the rate of Rs.15 per m is Rs.900. If the lengths of the triangle are in the ratio 3:4:5, find the area of the triangle and the cost of cultivating it at Rs.48 per kg sq.m.
Find the area of a triangle with a base 12cm and a height equal to the width of a rectangle having area of 96cm2 and a length of 12cm.
Find the perimeter of A scalene triangle with sides 7 m, 8 m, 10 m
