Advertisements
Advertisements
प्रश्न
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
उत्तर
In isosceles ∆ABC
AB = AC = 13 cm But perimeter = 50 cm
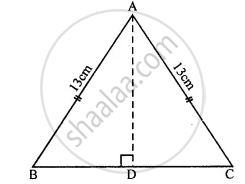
∴ BC = 50 - (13 + 13) cm
= 50 - 26 = 24 cm
AD ⊥ BC
∴ AD = DC = `24/2 = 12` cm.
In right ΔABD,
AB2 = AD2 + BD2 (Pythagoras Therorem)
`(13)^2 = "AD"^2 + (12)^2`
⇒ 169 = `"AD"^2 + 144`
⇒ `"AD"^2 = 169 - 144`
= 25 = (5)2
∴ AD = 5 cm.
Now area of ΔABC = `1/2 "Base" xx "Altitude"`
= `1/2 xx "BC" xx "AD"`
= `1/2 xx 24 xx 5 = 60` cm2
APPEARS IN
संबंधित प्रश्न
If the difference between the sides of a right-angled triangle is 3 cm and its area is 54 cm2; find its perimeter.
In triangle ABC; angle A = 90o, side AB = x cm, AC = (x + 5) cm and area = 150 cm2. Find the sides of the triangle.
Two sides of a triangle are 6 cm and 8 cm. If the height of the triangle corresponding to 6 cm side is 4 cm; find :
(i) area of the triangle
(ii) height of the triangle corresponding to 8 cm side.
The sides of a triangle are 16 cm, 12 cm, and 20 cm. Find :
(i) area of the triangle ;
(ii) height of the triangle, corresponding to the largest side ;
(iii) height of the triangle, corresponding to the smallest side.
Two sides of a triangle are 6.4 m and 4.8 m. If the height of the triangle corresponding to 4.8 m side is 6 m;
find :
(i) area of the triangle ;
(ii) height of the triangle corresponding to 6.4 m sides.
The base and the height of a triangle are in the ratio 4: 5. If the area of the triangle is 40 m2; find its base and height.
The area of an equilateral triangle is numerically equal to its perimeter. Find its perimeter correct to 2 decimal places.
A field is in the shape of a quadrilateral ABCD in which side AB = 18 m, side AD = 24 m, side BC = 40m, DC = 50 m and angle A = 90°. Find the area of the field.
Find the area of a triangle whose base is 3.8 cm and height is 2.8 cm.
Find the perimeter of An equilateral triangle with side 6 cm
