Advertisements
Advertisements
प्रश्न
The altitude and the base of a triangular field are in the ratio 6: 5. If its cost is ₹ 49,57,200 at the rate of ₹ 36,720 per hectare and 1 hectare = 10,000 sq. m, find (in metre) dimensions of the field.
उत्तर
Total cost = ₹ 49,57,200
Rate = ₹ 36,720 per hectare
The total area of the triangular field
= `4957200/36720 xx 10000 "m"^2 = 1350000 "m"^2`
The ratio in altitude and base of the field = 6: 5
Let altitude = 6x
and base = 5x
∴ Area = `1/2 "Base" xx "Altitude"`
⇒ 1350000 = `1/2 xx 5x xx 6x`
⇒ `15x^2 = 1350000 ⇒ x^2 = 1350000/15`
⇒ `x^2 = 90000 = (300)^2`
∴ x = 300
∴ Base = 5x = `5 xx 300 = 1500` m
and altitude = `6x = 6 xx 300 = 1800`m
APPEARS IN
संबंधित प्रश्न
AD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that ∠BOC = 90o. Find the area of quadrilateral ABOC.
The area of an equilateral triangle is 36`sqrt3` sq. cm. Find its perimeter.
The sides of a triangular field are in the ratio 5: 3: 4 and its perimeter is 180 m. Find:
(i) its area.
(ii) the altitude of the triangle corresponding to its largest side.
(iii) the cost of leveling the field at the rate of Rs. 10 per square meter.
The area of an equilateral triangle is `144sqrt3` cm2; find its perimeter.
The lengths of the sides of a triangle are in the ratio 4: 5 : 3 and its perimeter is 96 cm. Find its area.
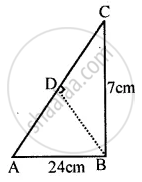
Use the information given in the adjoining figure to find :
(i) the length of AC.
(ii) the area of an ∆ABC
(iii) the length of BD, correct to one decimal place.
The perimeter of a triangle is 72cm and its sides are in the ratio 3:4:5. Find its area and the length of the altitude corresponding to the longest side.
The base of a triangle field and its height are in the ratio 2:5. If the cost of cultivating the field at Rs.42 per sq. m is Rs.7560, find its base and height.
The table given below contains some measures of the triangle. Find the unknown values.
| Side 1 | Side 2 | Side 3 | Perimeter |
| 6 cm | 5 cm | 2 cm | ? |
Find the perimeter and the area of a right angled triangle whose sides are 6 feet, 8 feet and 10 feet
