Advertisements
Advertisements
प्रश्न
The altitude and the base of a triangular field are in the ratio 6: 5. If its cost is ₹ 49,57,200 at the rate of ₹ 36,720 per hectare and 1 hectare = 10,000 sq. m, find (in metre) dimensions of the field.
उत्तर
Total cost = ₹ 49,57,200
Rate = ₹ 36,720 per hectare
The total area of the triangular field
= `4957200/36720 xx 10000 "m"^2 = 1350000 "m"^2`
The ratio in altitude and base of the field = 6: 5
Let altitude = 6x
and base = 5x
∴ Area = `1/2 "Base" xx "Altitude"`
⇒ 1350000 = `1/2 xx 5x xx 6x`
⇒ `15x^2 = 1350000 ⇒ x^2 = 1350000/15`
⇒ `x^2 = 90000 = (300)^2`
∴ x = 300
∴ Base = 5x = `5 xx 300 = 1500` m
and altitude = `6x = 6 xx 300 = 1800`m
APPEARS IN
संबंधित प्रश्न
Find the area of a triangle whose sides are 18 cm, 24 cm, and 30 cm. Also, find the length of altitude corresponding to the largest side of the triangle.
The base of a triangular field is three times its height. If the cost of cultivating the field at ₹ 36.72 per 100 m2 is ₹ 49,572; find its base and height.
Find the area and the perimeter of quadrilateral ABCD, given below; if AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and ∠DBC = 90°.
The perimeter of a triangle is 450 m and its side are in the ratio 12: 5: 13. Find the area of the triangle.
Two sides of a triangle are 6 cm and 8 cm. If the height of the triangle corresponding to 6 cm side is 4 cm; find :
(i) area of the triangle
(ii) height of the triangle corresponding to 8 cm side.
The base and the height of a triangle are in the ratio 5 : 3. If the area of the triangle is 67.5 m2; find its base and height.
A field is in the shape of a quadrilateral ABCD in which side AB = 18 m, side AD = 24 m, side BC = 40m, DC = 50 m and angle A = 90°. Find the area of the field.
Find the area of a triangle whose sides are in the ratio 5:12:13 and whose perimeter is 36cm.
The table given below contains some measures of the triangle. Find the unknown values.
| Side 1 | Side 2 | Side 3 | Perimeter |
| 11 feet | ? | 9 feet | 28 feet |
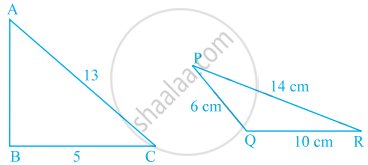
In the given figures, perimeter of ΔABC = perimeter of ΔPQR. Find the area of ΔABC.