Advertisements
Advertisements
प्रश्न
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
उत्तर
In isosceles ∆ABC
AB = AC = 13 cm But perimeter = 50 cm
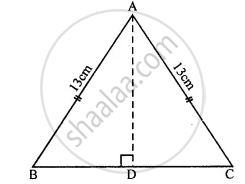
∴ BC = 50 - (13 + 13) cm
= 50 - 26 = 24 cm
AD ⊥ BC
∴ AD = DC = `24/2 = 12` cm.
In right ΔABD,
AB2 = AD2 + BD2 (Pythagoras Therorem)
`(13)^2 = "AD"^2 + (12)^2`
⇒ 169 = `"AD"^2 + 144`
⇒ `"AD"^2 = 169 - 144`
= 25 = (5)2
∴ AD = 5 cm.
Now area of ΔABC = `1/2 "Base" xx "Altitude"`
= `1/2 xx "BC" xx "AD"`
= `1/2 xx 24 xx 5 = 60` cm2
APPEARS IN
संबंधित प्रश्न
If the difference between the sides of a right-angled triangle is 3 cm and its area is 54 cm2; find its perimeter.
In triangle ABC; angle A = 90o, side AB = x cm, AC = (x + 5) cm and area = 150 cm2. Find the sides of the triangle.
Calculate the area and the height of an equilateral triangle whose perimeter is 60 cm.
Find the area and the perimeter of quadrilateral ABCD, given below; if AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and ∠DBC = 90°.
The given figure shows a right-angled triangle ABC and an equilateral triangle BCD. Find the area of the shaded portion.

The perimeter of a triangle is 450 m and its side are in the ratio 12: 5: 13. Find the area of the triangle.
The base and the height of a triangle are in the ratio 5 : 3. If the area of the triangle is 67.5 m2; find its base and height.
Find the area of the right-angled triangle with a hypotenuse of 40 cm and one of the other two sides of 24 cm.
Find the area of a triangle with a base 12cm and a height equal to the width of a rectangle having area of 96cm2 and a length of 12cm.
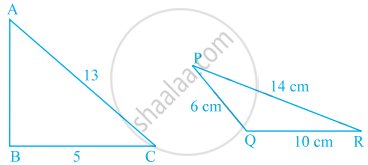
In the given figures, perimeter of ΔABC = perimeter of ΔPQR. Find the area of ΔABC.