Advertisements
Advertisements
Question
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
Solution
In isosceles ∆ABC
AB = AC = 13 cm But perimeter = 50 cm
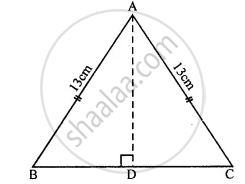
∴ BC = 50 - (13 + 13) cm
= 50 - 26 = 24 cm
AD ⊥ BC
∴ AD = DC = `24/2 = 12` cm.
In right ΔABD,
AB2 = AD2 + BD2 (Pythagoras Therorem)
`(13)^2 = "AD"^2 + (12)^2`
⇒ 169 = `"AD"^2 + 144`
⇒ `"AD"^2 = 169 - 144`
= 25 = (5)2
∴ AD = 5 cm.
Now area of ΔABC = `1/2 "Base" xx "Altitude"`
= `1/2 xx "BC" xx "AD"`
= `1/2 xx 24 xx 5 = 60` cm2
APPEARS IN
RELATED QUESTIONS
The base of a triangular field is three times its height. If the cost of cultivating the field at ₹ 36.72 per 100 m2 is ₹ 49,572; find its base and height.
Find the area of a triangle, whose sides are :
18 mm, 24 mm and 30 mm
The base and the height of a triangle are in the ratio 5 : 3. If the area of the triangle is 67.5 m2; find its base and height.
The area of an equilateral triangle is `144sqrt3` cm2; find its perimeter.
The area of an equilateral triangle is numerically equal to its perimeter. Find its perimeter correct to 2 decimal places.
Find the area of a triangle whose sides are 27 cm, 45 cm and 36 cm.
Find the perimeter of A scalene triangle with sides 7 m, 8 m, 10 m
A piece of wire is 36 cm long. What will be the length of each side if we form an equilateral triangle
A piece of string is 30 cm long. What will be the length of each side if the string is used to form an equilateral triangle?
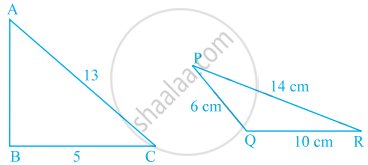
In the given figures, perimeter of ΔABC = perimeter of ΔPQR. Find the area of ΔABC.