Advertisements
Advertisements
Question
In the given figures, perimeter of ΔABC = perimeter of ΔPQR. Find the area of ΔABC.
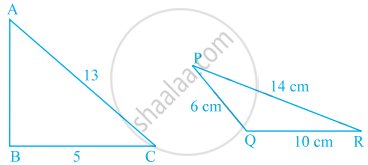
Solution
Given, perimeter of ΔABC = perimeter of ΔPQR
Perimeter of APQR = 14 + 6 + 10 = 30 cm ......[∵ Perimeter of triangle = sum of all sides]
Now, perimeter of ΔABC = AB + BC + CA
30 = AB + BC + AC
⇒ 30 = AB + 5 + 13
⇒ 30 = AB + 18
⇒ AB = 30 – 18 = 12 cm
∴ Area of ΔABC = `1/2` × Base × Height
= `1/2 xx 5 xx 12`
= 5 × 6
= 30 cm2
APPEARS IN
RELATED QUESTIONS
In triangle ABC; angle A = 90o, side AB = x cm, AC = (x + 5) cm and area = 150 cm2. Find the sides of the triangle.
ABC is a triangle in which AB = AC = 4 cm and ∠A = 90°. Calculate:
(i) The area of ΔABC,
(ii) The length of the perpendicular from A to BC.
Find the area of an isosceles triangle with perimeter is 36 cm and the base is 16 cm.
Find the area and the perimeter of quadrilateral ABCD, given below; if AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and ∠DBC = 90°.
Find the area of a triangle, whose sides are :
18 mm, 24 mm and 30 mm
Two sides of a triangle are 6.4 m and 4.8 m. If the height of the triangle corresponding to 4.8 m side is 6 m;
find :
(i) area of the triangle ;
(ii) height of the triangle corresponding to 6.4 m sides.
The area of an equilateral triangle is `144sqrt3` cm2; find its perimeter.
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
Find the area of a triangle whose base is 3.8 cm and height is 2.8 cm.
Find the perimeter and the area of a right angled triangle whose sides are 6 feet, 8 feet and 10 feet
