Advertisements
Advertisements
Question
ABC is a triangle in which AB = AC = 4 cm and ∠A = 90°. Calculate:
(i) The area of ΔABC,
(ii) The length of the perpendicular from A to BC.
Solution
(i) Area of the triangle is given by
A = `1/2 xx "AB" xx "AC"`
= `1/2 xx 4 xx 4`
= 8 sq .cm
Given the area as 8 sq. cm and using Pythagoras' theorem,
`BC=sqrt(AB^2+AC^2)`
`BC = sqrt(4^2+4^2) = sqrt(32)`
`BC = 4sqrt(2)`
(ii) Again area of the triangle
`A = 1/2 xx "BC" xx h`
`8 = 1/2 xx 4sqrt(2) xx h`
`8 = 2sqrt(2) xx h`
`h = 8/(2sqrt(2))xxsqrt(2)/sqrt(2)`
`h = (8sqrt(2))/4`
`h = 2sqrt(2)` cm
h = 2.83 cm
APPEARS IN
RELATED QUESTIONS
The base and the height of a triangle are in the ratio 4: 5. If the area of the triangle is 40 m2; find its base and height.
The area of an equilateral triangle is `144sqrt3` cm2; find its perimeter.
The area of an equilateral triangle is numerically equal to its perimeter. Find its perimeter correct to 2 decimal places.
A field is in the shape of a quadrilateral ABCD in which side AB = 18 m, side AD = 24 m, side BC = 40m, DC = 50 m and angle A = 90°. Find the area of the field.
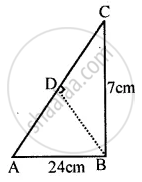
Use the information given in the adjoining figure to find :
(i) the length of AC.
(ii) the area of an ∆ABC
(iii) the length of BD, correct to one decimal place.
Find the area of a triangle whose sides are 27 cm, 45 cm and 36 cm.
The base of a triangle field and its height are in the ratio 2:5. If the cost of cultivating the field at Rs.42 per sq. m is Rs.7560, find its base and height.
The scalene triangle has 40 cm as its perimeter and whose two sides are 13 cm and 15 cm, find the third side
In the given figure, all triangles are equilateral and AB = 8 units. Other triangles have been formed by taking the mid points of the sides. What is the perimeter of the figure?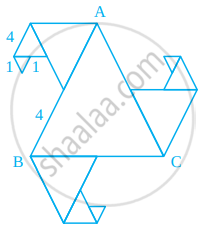
Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
