Advertisements
Advertisements
Question
Find the area of a triangle whose sides are 27 cm, 45 cm and 36 cm.
Solution
Let the sides of a triangle be a = 27cm, b = 45cm and c = 36cm
Semi-perimeter of a tirangle = s
= `("a" + "b" + "c")/(2)`
= `(27 + 45 + 36)/(2)`
= 54cm
Area of a triangle
= `sqrt("s"("s" - "a")("s" - "b")("s" - "c")`
= `sqrt(54(54 - 27)(54 - 45)(54 - 36)`
= `sqrt(54 xx 27 xx 9 xx 18)`
= `sqrt(6 xx 6 xx 3 xx 9 xx 9 xx 6 xx 3)`
= `sqrt(6 xx 6 xx 3 xx 3 xx 9 xx 9 xx 9)`
= 6 x 3 x 9 x 3
= 486cm2.
APPEARS IN
RELATED QUESTIONS
Find the area of a triangle whose sides are 18 cm, 24 cm, and 30 cm. Also, find the length of altitude corresponding to the largest side of the triangle.
The perimeter of a triangle is 450 m and its side are in the ratio 12: 5: 13. Find the area of the triangle.
The base and the height of a triangle are in the ratio 4: 5. If the area of the triangle is 40 m2; find its base and height.
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
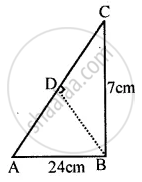
Use the information given in the adjoining figure to find :
(i) the length of AC.
(ii) the area of an ∆ABC
(iii) the length of BD, correct to one decimal place.
The perimeter of a triangle is 72cm and its sides are in the ratio 3:4:5. Find its area and the length of the altitude corresponding to the longest side.
Find the area of a right angled triangle whose hypotenuse is 15cm and the base is 9cm.
The cost of fencing a triangular field at the rate of Rs.15 per m is Rs.900. If the lengths of the triangle are in the ratio 3:4:5, find the area of the triangle and the cost of cultivating it at Rs.48 per kg sq.m.
The table given below contains some measures of the triangle. Find the unknown values.
| Side 1 | Side 2 | Side 3 | Perimeter |
| 6 cm | 5 cm | 2 cm | ? |
Find the perimeter of the triangle, whose sides are 13 cm, 5 cm and 14 cm
