Advertisements
Advertisements
Question
Find the area of an isosceles triangle ABC in which AB = AC = 6 cm, ∠A = 90°. Also, find the length of perpendicular from A to BC.
Solution
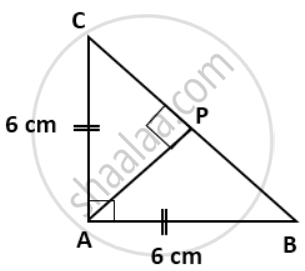
Area of ΔABC
= `(1)/(2) xx "AB" xx "AC"`
= `(1)/(2) xx 6 xx 6`
= 18cm2.
In right-angled ΔBAC,
BC2
= AB2 + AC2
= 62 + 62
= 36 + 36
= 72
⇒ BC = `6sqrt(2)"cm"`
Now,
area of ΔABC is also
= `(1)/(2) xx "BC" xx "AP"`
⇒ 18 = `(1)/(2) xx 6sqrt(2) xx "AP"`
⇒ 18 = `3sqrt(2) xx "AP"`
⇒ AP
= `(18)/(3sqrt(2)`
= `(6)/sqrt(2)`
= `(6)/sqrt(2) xx sqrt(2)/sqrt(2)`
= `(6sqrt(2))/(2)`
= `3sqrt(2)"cm"`.
APPEARS IN
RELATED QUESTIONS
Find the area of an equilateral triangle of side 20 cm.
Find the perimeter of an equilateral triangle whose area is `16sqrt(3)"cm"`.
The area of an equilateral triangle is numerically equal to its perimeter. Find the length of its sides, correct two decimal places.
In a right-angled triangle ABC, if ∠B = 90°, AB - BC = 2 cm; AC - BC = 4 and its perimeter is 24 cm, find the area of the triangle.
In a right-angled triangle ABC, if ∠B = 90°, AB - BC = 2 cm; AC - BC = 4 and its perimeter is 24 cm, find the area of the triangle.
A wire when bent in the form of a square encloses an area of 16 cm2. Find the area enclosed by it when the same wire is bent in the form of a rectangle whose sides are in the ratio of 1 : 3
A wire when bent in the form of a square encloses an area of 16 cm2. Find the area enclosed by it when the same wire is bent in the form of an equilateral triangle
If in an isosceles triangle, each of the base angles is 40°, then the triangle is ______.
In an isosceles triangle, two angles are always ______.
Two line segments are congruent, if they are of ______ lengths.
