Advertisements
Advertisements
Question
The area of an equilateral triangle is numerically equal to its perimeter. Find its perimeter correct to 2 decimal places.
Solution 1
Let each side of the equilateral triangle = x
∴ Its area = `sqrt(3)/4 x^2`
Area perimeter = 3x
By the given condition = `sqrt(3)/4 x^2 = 3x`
`x^2 = 3x xx 4/sqrt(3)`
`x^2 = (3x xx 4 xx sqrt(3))/(sqrt(3) xx sqrt(3)) = (3x xx 4 xx sqrt(3))/3 = 4xsqrt(3)`
⇒ `x^2 = sqrt(3) (4x) ⇒ x = 4sqrt(3)` [∵ x ≠ 0]
∴ Perimeter = `12sqrt(3)` units
= 12 (1.732) = 20.784 = 20.78 units
Solution 2
Let the side length of the equilateral triangle be a.
Step 1: Write the formula for the area and the perimeter
- Area of an equilateral triangle: Area = `sqrt3/4 a^2`
- Perimeter of the triangle: Perimeter = 3a
Step 2: Given that the area equals the perimeter
`sqrt3/4 a^2 = 3a`
Step 3: Simplify the equation
Divide through by a (assuming a ≠ 0): `sqrt3/4 a = 3`
Multiply through by 4: `sqrt3 a = 12`
Divide by `sqrt3`: `a = 12/sqrt3`
Rationalize the denominator: `a = (12sqrt3)/3 = 4sqrt3`
Step 4: Calculate the perimeter
Perimeter = 3a
`= 3(4sqrt3) = 12sqrt3`
Step 5: Approximate to 2 decimal places
Using `sqrt3 = 1.732`
12√3 = 12 × 1.732 = 20.784
= 20.784
APPEARS IN
RELATED QUESTIONS
AD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that ∠BOC = 90o. Find the area of quadrilateral ABOC.
In triangle ABC; angle A = 90o, side AB = x cm, AC = (x + 5) cm and area = 150 cm2. Find the sides of the triangle.
The length of the sides of a triangle are in the ratio 3: 4: 5. Find the area of the triangle if its perimeter is 144 cm.
The sides of a triangle are 16 cm, 12 cm, and 20 cm. Find :
(i) area of the triangle ;
(ii) height of the triangle, corresponding to the largest side ;
(iii) height of the triangle, corresponding to the smallest side.
Find the area of a triangle whose sides are 27 cm, 45 cm and 36 cm.
Find the area of a triangle with a base 12cm and a height equal to the width of a rectangle having area of 96cm2 and a length of 12cm.
Find the perimeter and the area of a right angled triangle whose sides are 6 feet, 8 feet and 10 feet
Find the perimeter of An equilateral triangle with side 6 cm
In the given figure, all triangles are equilateral and AB = 8 units. Other triangles have been formed by taking the mid points of the sides. What is the perimeter of the figure?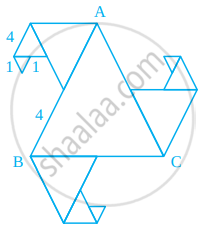
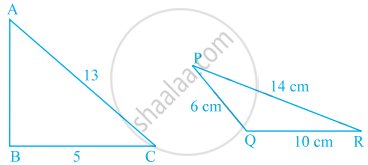
In the given figures, perimeter of ΔABC = perimeter of ΔPQR. Find the area of ΔABC.