Advertisements
Advertisements
Question
The sides of a triangle are 16 cm, 12 cm, and 20 cm. Find :
(i) area of the triangle ;
(ii) height of the triangle, corresponding to the largest side ;
(iii) height of the triangle, corresponding to the smallest side.
Solution
Sides of ∆ are
a = 20 cm
b = 12 cm
c = 16 cm
`S = (a + b + c)/2`
= `(20 + 12 + 16)/2`
= `48/2 = 24`
area of Δ = `sqrt(s(s - a)(s - b)(s - c))`
= `sqrt(24(24 - 20)(24 - 12)(24 - 16))`
= `sqrt(24 xx 4 xx 12 xx 8)`
= `sqrt(12 xx 2 xx 4 xx 12 xx 2 xx 4)`
= `sqrt(12 xx 12 xx 4 xx 4 xx 2 xx 2)`
= `12 xx 4 xx 2 = 96 "cm"^2`
AD is height of Δ corresponding to largest side.
∴ `1/2 xx "BC" xx "AD" = 96`
`1/2 xx 20 xx "AD" = 96`
AD = `(96 xx 2)/20`
AD = 9.6 cm
BE is height of Δ corresponding to smallest side.
∴ `1/2 "AC" xx "BE" = 96`
`1/2 xx 12 xx "BE" = 96`
BE = `(96 xx 2)/12`
BE = 16 cm
(i) 96 cm2 (ii) 9.6 cm (iii) 16 cm
APPEARS IN
RELATED QUESTIONS
AD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that ∠BOC = 90o. Find the area of quadrilateral ABOC.
Find the area of a triangle, whose sides are :
10 cm, 24 cm, and 26 cm
Two sides of a triangle are 6.4 m and 4.8 m. If the height of the triangle corresponding to 4.8 m side is 6 m;
find :
(i) area of the triangle ;
(ii) height of the triangle corresponding to 6.4 m sides.
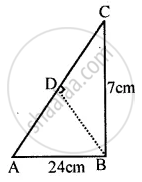
Use the information given in the adjoining figure to find :
(i) the length of AC.
(ii) the area of an ∆ABC
(iii) the length of BD, correct to one decimal place.
Find the area of a triangle whose sides are in the ratio 5:12:13 and whose perimeter is 36cm.
The perimeter of a triangle is 72cm and its sides are in the ratio 3:4:5. Find its area and the length of the altitude corresponding to the longest side.
Find the area of a triangle with a base 12cm and a height equal to the width of a rectangle having area of 96cm2 and a length of 12cm.
The perimeter of a triangle is 28 cm. One of it’s sides is 8cm. Write all the sides of the possible isosceles triangles with these measurements.
Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
Area of an isosceles triangle is 48 cm2. If the altitudes corresponding to the base of the triangle is 8 cm, find the perimeter of the triangle.
