Advertisements
Advertisements
Question
The perimeter of a triangle is 28 cm. One of it’s sides is 8cm. Write all the sides of the possible isosceles triangles with these measurements.
Solution
Let ∆ABC be an isosceles triangle, where AB = 8 cm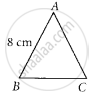
Case I: If AB = BC
AB = BC = 8 cm
Perimeter of the triangle ABC = 28 cm
⇒ AB + BC + CA = 28 cm
⇒ 8 cm + 8 cm + CA = 28 cm
⇒ 16 cm + CA = 28 cm
⇒ CA = 28 cm – 16 cm = 12 cm
∴ Sides are 8 cm, 8 cm and 12 cm
Case II: If BC = CA
Perimeter of the triangle ABC = 28 cm
⇒ AB + BC + CA = 28 cm
8 cm + 2BC = 28 cm
⇒ 2BC = 28 cm – 8cm = 20 cm
⇒ BC = 10 cm
∴ Sides are 10 cm, 10 cm and 8 cm
APPEARS IN
RELATED QUESTIONS
Calculate the area and the height of an equilateral triangle whose perimeter is 60 cm.
Find the area and the perimeter of quadrilateral ABCD, given below; if AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and ∠DBC = 90°.
The given figure shows a right-angled triangle ABC and an equilateral triangle BCD. Find the area of the shaded portion.

Find the area of a triangle, whose sides are :
21 m, 28 m, and 35 m
Two sides of a triangle are 6 cm and 8 cm. If the height of the triangle corresponding to 6 cm side is 4 cm; find :
(i) area of the triangle
(ii) height of the triangle corresponding to 8 cm side.
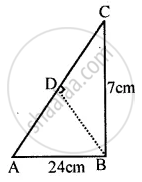
Use the information given in the adjoining figure to find :
(i) the length of AC.
(ii) the area of an ∆ABC
(iii) the length of BD, correct to one decimal place.
Find the perimeter and the area of a right angled triangle whose sides are 6 feet, 8 feet and 10 feet
The scalene triangle has 40 cm as its perimeter and whose two sides are 13 cm and 15 cm, find the third side
A piece of wire is 36 cm long. What will be the length of each side if we form an equilateral triangle
Area of an isosceles triangle is 48 cm2. If the altitudes corresponding to the base of the triangle is 8 cm, find the perimeter of the triangle.
