Advertisements
Advertisements
Question
Find the area of a triangle, whose sides are :
21 m, 28 m, and 35 m
Solution
Sides of ∆ are
a = 21 m
b = 28 m
c = 35 m
S = `(a + b + c)/2 = (21 + 28 + 35)/2`
= `84/2 = 42`
area of Δ = `sqrt(S(S - a)(S - b)(S - c))`
= `sqrt(42(42 - 21)(42 - 28)(42 - 35))`
= `sqrt(42 xx 21 xx 14 xx 7)`
= `sqrt(7 xx 3 xx 2 xx 3 xx 7 xx 2 xx 7 xx 7)`
= `sqrt(7 xx 7 xx 7 xx 7 xx 3 xx 3 xx 2 xx 2)`
= `7 xx 7 xx 3 xx 2 = 294 "m"^2`
APPEARS IN
RELATED QUESTIONS
In triangle ABC; angle A = 90o, side AB = x cm, AC = (x + 5) cm and area = 150 cm2. Find the sides of the triangle.
The length of the sides of a triangle are in the ratio 3: 4: 5. Find the area of the triangle if its perimeter is 144 cm.
The sides of a triangle are 16 cm, 12 cm, and 20 cm. Find :
(i) area of the triangle ;
(ii) height of the triangle, corresponding to the largest side ;
(iii) height of the triangle, corresponding to the smallest side.
The lengths of the sides of a triangle are in the ratio 4: 5 : 3 and its perimeter is 96 cm. Find its area.
Find the area of the right-angled triangle with a hypotenuse of 40 cm and one of the other two sides of 24 cm.
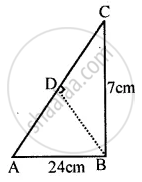
Use the information given in the adjoining figure to find :
(i) the length of AC.
(ii) the area of an ∆ABC
(iii) the length of BD, correct to one decimal place.
Find the area of a triangle whose base is 3.8 cm and height is 2.8 cm.
The perimeter of a triangle is 72cm and its sides are in the ratio 3:4:5. Find its area and the length of the altitude corresponding to the longest side.
The table given below contains some measures of the triangle. Find the unknown values.
| Side 1 | Side 2 | Side 3 | Perimeter |
| ? | 8 m | 3 m | 17 m |
Find the perimeter and the area of a right angled triangle whose sides are 6 feet, 8 feet and 10 feet
