Advertisements
Advertisements
Question
A field is in the shape of a quadrilateral ABCD in which side AB = 18 m, side AD = 24 m, side BC = 40m, DC = 50 m and angle A = 90°. Find the area of the field.
Solution
Since ∠A = 90°
By Pythagorus Theorem,
In ∆ABD,
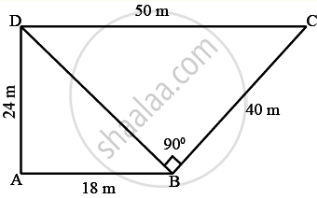
Now, the area of ΔABD = `1/2 (18)(24)`
= (18) (12) = 216 m2
In ΔABD
BD = `sqrt("AB"^2 + "AD"^2) = sqrt(18^2 + 24^2)`
= `sqrt(324 + 576) = sqrt(900) = 30`m.
S = `120/20 = 60 cm^2`
=`sqrt( 60xx10xx20xx30)`
= `sqrt(10xx2xx3xx10xx10xx2xx10xx3)`
= 10 × 10 × 6
= 600 cm2
Area of quadrilateral ABCD
= 816cm2
APPEARS IN
RELATED QUESTIONS
ABC is a triangle in which AB = AC = 4 cm and ∠A = 90°. Calculate:
(i) The area of ΔABC,
(ii) The length of the perpendicular from A to BC.
The given figure shows a right-angled triangle ABC and an equilateral triangle BCD. Find the area of the shaded portion.

Two sides of a triangle are 6 cm and 8 cm. If the height of the triangle corresponding to 6 cm side is 4 cm; find :
(i) area of the triangle
(ii) height of the triangle corresponding to 8 cm side.
The base and the height of a triangle are in the ratio 4: 5. If the area of the triangle is 40 m2; find its base and height.
Find the area of the right-angled triangle with a hypotenuse of 40 cm and one of the other two sides of 24 cm.
Find the area of a triangle with a base 12cm and a height equal to the width of a rectangle having area of 96cm2 and a length of 12cm.
Find the perimeter and the area of a right angled triangle whose sides are 6 feet, 8 feet and 10 feet
From one vertex of an equilateral triangle with side 40 cm, an equilateral triangle with 6 cm side is removed. What is the perimeter of the remaining portion?
Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.
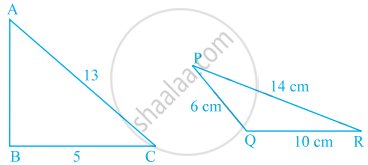
In the given figures, perimeter of ΔABC = perimeter of ΔPQR. Find the area of ΔABC.