Advertisements
Advertisements
प्रश्न
The sides of a triangular field are in the ratio 5: 3: 4 and its perimeter is 180 m. Find:
(i) its area.
(ii) the altitude of the triangle corresponding to its largest side.
(iii) the cost of leveling the field at the rate of Rs. 10 per square meter.
उत्तर १
(i) Given that the sides of a triangle are in the ratio 5: 3: 4.
Also, given that the perimeter of the triangle is 180.
Thus, we have, 5x + 4x + 3x = 180
⇒ 12x = 180
⇒ x = `180/12`
⇒ x = 15.
Thus, the sides are 5 × 15, 3 × 15 and 4 × 15
That is the sides are 75 m, 45 m and 60 m.
Since the sides are in the ratio, 5: 3: 4, it is a Pythagorean triplet,
Therefore, the triangle is a right-angled triangle,
Area of a right-angled triangle = `1/2` × base × altitude
⇒ `1/2`× 45 × 60
⇒ 45 × 30
= 1350 m2.
(ii) Consider the following figure.
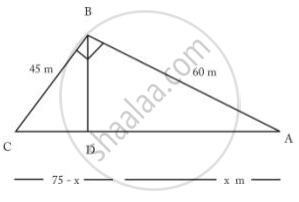
In the above figure,
The largest side is AC = 75 m,
The altitude corresponding to AC is BD.
We need to find the value of BD.
Now consider the triangles ΔBCD and ΔBAD.
We have,
∠B = ∠B .....[common]
BD = BD .....[common]
∠D = ∠D = 90°
Thus, by Angle-Side-Angle criterion of congruence,
we have ΔBCD - ΔABD,
Similar triangles have similar proportionality.
Thus, we have,
`"CD"/"BD" = "BD"/"AD"`
⇒ BD2 = AD × CD ....(1)
From subpart (i), the sides of the triangle are AC = 75 m, AB = 60 m and BC = 45 m
Let AD = x m ⇒ CD = (75 - x) m
Thus applying Pythagoras Theorem,
from right triangle ΔBCD, we have
452 = (75 - x)2 + BD2
⇒ BD2 = 452 - (75 - x)2
⇒ BD2 = 2025 - (5625 + x2 - 150x)
⇒ BD2 = 2025 - 5625 - x2 + 150x
⇒ BD2 = - 3600 - x2 + 150x ....(2)
Now applying Pythagoras Theorem,
from right triangle ΔABD, we have
602 = x2 + BD2
⇒ BD2 = 602 - x2
⇒ BD2 = 3600 - x2 ......(3)
From equations (2) and (3), we have,
- 3600 - x2 + 150x = 3600 -x2
⇒ 150x = 3600 + 3600
⇒ 150x = 7200
⇒ x = `7200/150`
⇒ x = 48
Thus, AD = 48 and CD = 75 - 48 = 27.
Substituting the values AD = 48 m
and CD = 27 m in equation (1), we have
BD2 = 48 x 27
⇒ BD2 = 1296
⇒ BD = 36 m
The altitude of the triangle corresponding to
its largest side is BD = 36 m
(iii) The area of the triangular field from subpart (i) is 1350 m2
The cost of levelling the field is Rs. 10 per square metre,
Thus the total cost of levelling the field = 1350 x 10 = Rs. 13,500.
उत्तर २
a = 5x = 5(15) = 75 m
b = 3x = 3(15) = 45 m
c = 4x = 4(15) = 60 m
P = 180 m
5x + 3x + 4x = 180
12x = 180
x = `180/12 = 15`
S = `180/2` = 90
ar(ABC) = `sqrt("s"("s - a")("s" - "b")("s" - "c"))`
`= sqrt(90(90 - 75)(90 - 45)(90- 60))`
`= sqrt(90 xx 15 xx 45 xx 30)`
`= sqrt(9 xx 10 xx 3 xx 5 xx 9 xx 5 xx 3 xx 10)`
`= 9 xx 5 xx 3 xx 10`
= 1350 m2
ar(Δ ABC) = 1350
`1/2 xx "b" xx "h" = 1350`
`1/2 xx 75 xx "h"`= 1350
h = `(1350 xx 2)/75`
h = 18 × 2
h = 36 m
∴ Cost of leveling = 1350 × 10 = 13500
APPEARS IN
संबंधित प्रश्न
Find the area of a triangle whose sides are 18 cm, 24 cm, and 30 cm. Also, find the length of altitude corresponding to the largest side of the triangle.
Find the area and the perimeter of quadrilateral ABCD, given below; if AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and ∠DBC = 90°.
Find the area of the right-angled triangle with a hypotenuse of 40 cm and one of the other two sides of 24 cm.
Find the area of a right angled triangle whose hypotenuse is 15cm and the base is 9cm.
The table given below contains some measures of the triangle. Find the unknown values.
| Side 1 | Side 2 | Side 3 | Perimeter |
| ? | 8 m | 3 m | 17 m |
The table given below contains some measures of the triangle. Find the unknown values.
| Side 1 | Side 2 | Side 3 | Perimeter |
| 11 feet | ? | 9 feet | 28 feet |
Find the perimeter of An equilateral triangle with side 6 cm
Find the perimeter of the triangle, whose sides are 13 cm, 5 cm and 14 cm
The perimeter of a triangle is 28 cm. One of it’s sides is 8cm. Write all the sides of the possible isosceles triangles with these measurements.
Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.
