Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 20 - Area and Perimeter of Plane Figures [Latest edition]

Find the area of a triangle whose sides are 18 cm, 24 cm, and 30 cm. Also, find the length of altitude corresponding to the largest side of the triangle.

The length of the sides of a triangle are in the ratio 3: 4: 5. Find the area of the triangle if its perimeter is 144 cm.

ABC is a triangle in which AB = AC = 4 cm and ∠A = 90°. Calculate:
(i) The area of ΔABC,
(ii) The length of the perpendicular from A to BC.

The area of an equilateral triangle is 36`sqrt3` sq. cm. Find its perimeter.

Find the area of an isosceles triangle with perimeter is 36 cm and the base is 16 cm.

The base of an isosceles triangle is 24 cm and its area is 192 sq. cm. Find its perimeter.

The given figure shows a right-angled triangle ABC and an equilateral triangle BCD. Find the area of the shaded portion.

Find the area and the perimeter of quadrilateral ABCD, given below; if AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and ∠DBC = 90°.

The base of a triangular field is three times its height. If the cost of cultivating the field at ₹ 36.72 per 100 m² is ₹ 49,572; find its base and height.

The sides of a triangular field are in the ratio 5: 3: 4 and its perimeter is 180 m. Find:

(i) its area.

(ii) the altitude of the triangle corresponding to its largest side.

(iii) the cost of leveling the field at the rate of Rs. 10 per square meter.

Each of the equal sides of an isosceles triangle is 4 cm greater than its height. If the base of the triangle is 24 cm; calculate the perimeter and the area of the triangle.

Calculate the area and the height of an equilateral triangle whose perimeter is 60 cm.

In triangle ABC; angle A = 90^o, side AB = x cm, AC = (x + 5) cm and area = 150 cm². Find the sides of the triangle.

If the difference between the sides of a right-angled triangle is 3 cm and its area is 54 cm²; find its perimeter.

AD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that ∠BOC = 90^o. Find the area of quadrilateral ABOC.

Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively. 

The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.

Calculate the area of quadrilateral ABCD, in which ∠ABD = 90°, triangle BCD is an equilateral triangle of side 24 cm and AD = 26 cm.

Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm ∠A = 90° and BC = CD = 52 cm.

The perimeter of a rectangular field is `3/5`km. If the length of the field is twice its width; find the area of the rectangle in sq. meters.

A rectangular plot 85 m long and 60 m broad is to be covered with grass leaving 5 m all around. Find the area to be laid with grass. 

The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.

How many tiles, each of area 400 cm², will be needed to pave a footpath which is 2 m wide and surrounds a grass plot 25 m long and 13 m wide? 

The cost of enclosing a rectangular garden with a fence all around, at the rate of 75 paise per metre, is Rs. 300. If the length of the garden is 120 metres, find the area of the field in square metres. 

The width of a rectangular room is `4/7`of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.

The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.

(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement

(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah. 

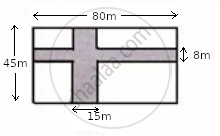
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion. 

The rate for a 1.20 m wide carpet is Rs. 40 per meter; find the cost of covering a hall 45 m long and 32 m wide with this carpet. Also, find the cost of carpeting the same hall if the carpet, 80 wide, is at Rs. 25. Per meter. 

Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 meters. Given your answer correct to 2 places of decimals. 

The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.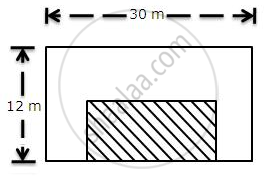

(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.

A floor that measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm. Find the number of tiles required.
Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is left uncovered?

Two adjacent sides of a parallelogram are 24 cm and 18 cm. If the distance between the longer sides is 12 cm; find the distance between the shorter sides.

Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.

The area of a rhombus is 216 sq. cm. If it's one diagonal is 24 cm; find:
(i) Length of its other diagonal,
(ii) Length of its side,
(iii) The perimeter of the rhombus.

The perimeter of a rhombus is 52 cm. If one diagonal is 24 cm; find:
(i) The length of its other diagonal,
(ii) Its area.

The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.

The figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 cm, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.

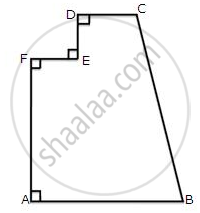
Calculate the area of the figure given below: which is not drawn scale.

The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH, and HD are 50 m, 40 m, 15 m and 25 m, respectively, and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.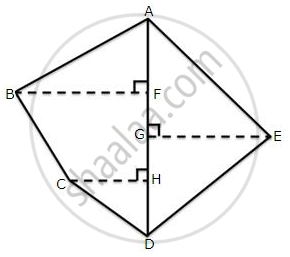

A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m², find its width.

A wire when bent in the form of a square encloses an area of 484 m². Find the largest area enclosed by the same wire when bent to from:

1. An equilateral triangle.
2. A rectangle of length 16 m.

Trapezium given below; find its area.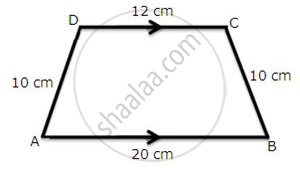

Trapezium given below; find its area.

 Trapezium given below; find its area.

Trapezium given below; find its area.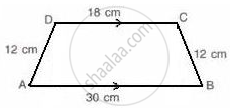

The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm²; find its dimensions.

The area of a rectangular is 640 m². Taking its length as x cm; find in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.

The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.

ABCD is a square with each side 12 cm. P is a point on BC such that area of  ΔABP: area of trapezium APCD = 1: 5. Find the length of CP.

A rectangular plot of land measures 45 m x 30 m. A boundary wall of height 2.4 m is built all around the plot at a distance of 1 m from the plot. Find the area of the inner surface of the boundary wall.

A wire when bent in the form of a square encloses an area = 576 cm². Find the largest area enclosed by the same wire when bent to form;
(i) an equilateral triangle.
(ii) A rectangle whose adjacent sides differ by 4 cm.

The area of a parallelogram is y cm² and its height is h cm. The base of another parallelogram is x cm more than the base of the first parallelogram and its area is twice the area of the first. Find, in terms of y, h, and x, the expression for the height of the second parallelogram.

The distance between parallel sides of a trapezium is 15 cm and the length of the line segment joining the mid-points of its non-parallel sides is 26 cm. Find the area of the trapezium.

The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.

The diameter of a circle is 28 cm.
Find its :
(i) Circumference
(ii) Area.

The circumference of a circular field is 308 m. Find is:
(i) Radius
(ii) Area.

The sum of the circumference and diameter of a circle is 116 cm. Find its radius. 

The radii of two circles are 25 cm and 18 cm. Find the radius of the circle which has a circumference equal to the sum of circumferences of these two circles. 

The radii of two circles are 48 cm and 13 cm. Find the area of the circle which has its circumference equal to the difference of the circumferences of the given two circles.

The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.

The radius of a circle is 5 m. Find the circumference of the circle whose area is 49 times the area of the given circle.

A circle of the largest area is cut from a rectangular piece of cardboard with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.

The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.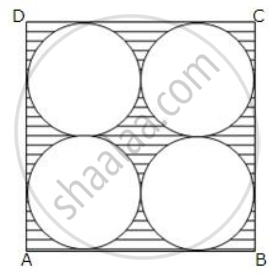

Find the area of the remaining card-board.

The radii of two circles are in the ratio 3: 8. If the difference between their areas is 2695π cm², find the area of the smaller circle. 

The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.

Find the area of a ring-shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.

The circumference of a given circular park is 55 m. It is surrounded by a path of uniform width of 3.5 m. Find the area of the path.

There are two circular gardens A and B. The circumference of garden A is 1.760 km and the area of garden B is 25 times the area of garden A. Find the circumference of garden B.

A wheel has a diameter of 84 cm. Find how many completer revolutions must it make to cover 3.168 km.

Each wheel of a car is of diameter 80 cm. How many completer revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour?

An express train is running between two stations with a uniform speed. If the diameter of each wheel of the train is 42 cm and each wheel makes 1200 revolutions per minute, find the speed of the train.

The minute hand of a clock is 8 cm long. Find the area swept by the minute hand between 8.30 a.m. and 9.05 a.m.

The shaded portion of the figure, given alongside, shows two concentric circles. If the circumference of the two circles is 396 cm and 374 cm, find the area of the shaded portion.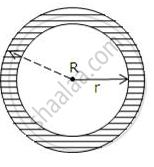

In the given figure, the area of the shaded portion is 770 cm². If the circumference of the outer circle is 132 cm, find the width of the shaded portion.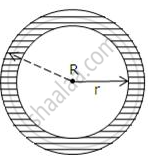

The cost of fencing a circular field at the rate of ₹ 240 per meter is ₹ 52,800. The field is to be ploughed at the rate of ₹ 12.50 per m². Find the cost of pouching the field.

Two circles touch each other externally. The sum of their areas is 58π cm² and the distance between their centers is 10 cm. Find the radii of the two circles.

The given figures show a rectangle ABCD inscribed in a circle as shown alongside.
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.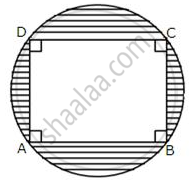

A square is inscribed in a circle of radius 7 cm. Find the area of the square.

A metal wire, when bent in the form of an equilateral triangle of largest area, encloses an area of 484 `sqrt3` cm². If the same wire is bent into the form of a circle of largest area, find the area of this circle.

The perimeter of a triangle is 450 m and its side are in the ratio 12: 5: 13. Find the area of the triangle.

A triangle and a parallelogram have the same base and the same area. If the side of the triangle is 26 cm, 28 cm, and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.

Using the information in the following figure, find its area.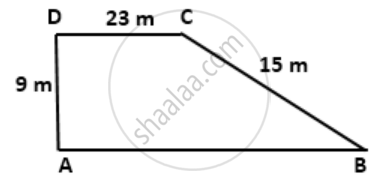

Sum of the areas of two squares is 400 cm². If the difference of their perimeters is 16 cm, find the sides of the two squares. 

Find the area and the perimeter of a square with diagonal 24 cm. [Take √2 = 1.41 ] 

A steel wire, when bent in the form of a square, encloses an area of 121 cm². The same wire is bent in the form of a circle. Find area the circle. 

The perimeter of a semicircular plate is 108 cm. find its area. 

Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.

The diameters of the front and the rear wheels of a tractor are 63 cm and 1.54 m respectively. The rear wheel is rotating at `24 6/11` revolutions per minute. Find:
(i) the revolutions per minute made by the front wheel.
(ii) the distance traveled bu the tractor in 40 minutes.

Two circles touch each other externally. The sum of their areas is 74π cm² and the distance between their centers is 12 cm. Find the diameters of the circle.

If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.