Advertisements
Advertisements
प्रश्न
AD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that ∠BOC = 90o. Find the area of quadrilateral ABOC.
उत्तर

Area of ΔABC =`"b"/4 sqrt(4"a"^2 - "b"^2)`
`= 36/4 xx sqrt( 4 xx 30^2 - 36^2 )`
= `9 xx sqrt2304`
= 9 × 48
= 432 cm2
∠ BOD = ∠ COD = 45°
OB = OC = x
In Δ BOC,
`"H"^2 = "P"^2 + "B"^2`
`(36)^2 = x^2 + x^2`
`36 xx 36 = 2x^2`
`sqrt(36 xx 18)` = x
`sqrt(6 xx 6 xx 3 xx 3 xx 2)` = x
∴ x = `18sqrt2`
Now,
Area of ΔBOC = `1/2 xx "base" xx "height"`
`= 1/2 xx 18sqrt2 xx 18sqrt2`
`= 162 xx 2`
= 324 cm2
Area of ABOC = Area of ΔABC - Area of ΔBOC
= 432 - 324
= 108 cm2
APPEARS IN
संबंधित प्रश्न
The base of a triangular field is three times its height. If the cost of cultivating the field at ₹ 36.72 per 100 m2 is ₹ 49,572; find its base and height.
The perimeter of a triangle is 450 m and its side are in the ratio 12: 5: 13. Find the area of the triangle.
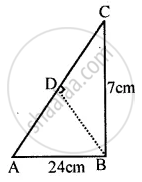
Use the information given in the adjoining figure to find :
(i) the length of AC.
(ii) the area of an ∆ABC
(iii) the length of BD, correct to one decimal place.
The base of a triangle field and its height are in the ratio 2:5. If the cost of cultivating the field at Rs.42 per sq. m is Rs.7560, find its base and height.
Find the area of a triangle with a base 12cm and a height equal to the width of a rectangle having area of 96cm2 and a length of 12cm.
Find the area of a triangle with a base 12cm and a height equal to the width of a rectangle having area of 96cm2 and a length of 12cm.
The table given below contains some measures of the triangle. Find the unknown values.
| Side 1 | Side 2 | Side 3 | Perimeter |
| 11 feet | ? | 9 feet | 28 feet |
Find the perimeter of An isosceles triangle with equal sides 10 cm each and third side is 7 cm
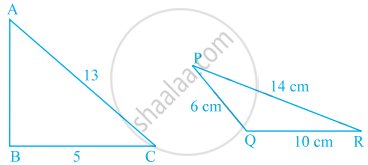
In the given figures, perimeter of ΔABC = perimeter of ΔPQR. Find the area of ΔABC.
Area of an isosceles triangle is 48 cm2. If the altitudes corresponding to the base of the triangle is 8 cm, find the perimeter of the triangle.
