Advertisements
Advertisements
प्रश्न
The width of a rectangular room is `4/7`of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
उत्तर
Length of the rectangle = x
Width of the rectangle = `4/7` x
Hence its perimeter is given by
2` ( x + 4/7 x )` = y
2`(( 11x) /7)` =y
`(22x)/7` = y
Again it is given that the perimeter is 4400cm.
Hence
`(22x)/7` = 4400
x = 1400
Length of the rectangle = 1400 cm = 14 m
APPEARS IN
संबंधित प्रश्न
The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to from:
- An equilateral triangle.
- A rectangle of length 16 m.
The cost of enclosing a rectangular garden with a fence all around, at the rate of 75 paise per metre, is Rs. 300. If the length of the garden is 120 metres, find the area of the field in square metres.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
The perimeter of a rhombus is 52 cm. If one diagonal is 24 cm; find:
(i) The length of its other diagonal,
(ii) Its area.
The area of a rhombus is 216 sq. cm. If it's one diagonal is 24 cm; find:
(i) Length of its other diagonal,
(ii) Length of its side,
(iii) The perimeter of the rhombus.
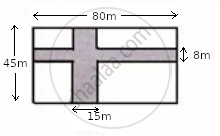
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
Let P(11, 7), Q(13.5, 4) and R(9.5, 4) be the midpoints of the sides AB, BC and AC respectively of ∆ABC. Find the coordinates of the vertices A, B and C. Hence find the area of ∆ABC and compare this with area of ∆PQR.
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
