Advertisements
Advertisements
प्रश्न
The area of a rhombus is 216 sq. cm. If it's one diagonal is 24 cm; find:
(i) Length of its other diagonal,
(ii) Length of its side,
(iii) The perimeter of the rhombus.
उत्तर
(i) We know that,
Area of Rhombus = `1/2` x AC x BD
Here
A = 216 sq.cm
AC = 24 cm
BD = ?
Now,
A = `1/2` x AC x BD
216 = `1/2` x 24 x BD
BD = 18 cm.
(ii) Let a be the length of each side of the rhombus.
a2 = `("AC"/2 )^2 + ("BD"/2)^2`
a2 = 122 + 92
a2 = 225
a = 15 cm
(iii) Perimeter of the rhombus = 4a = 60 cm.
APPEARS IN
संबंधित प्रश्न
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
A rectangular plot 85 m long and 60 m broad is to be covered with grass leaving 5 m all around. Find the area to be laid with grass.
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
The perimeter of a rhombus is 52 cm. If one diagonal is 24 cm; find:
(i) The length of its other diagonal,
(ii) Its area.
Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.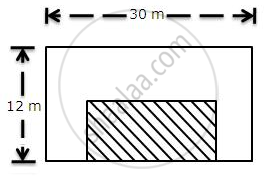
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
Find the area and the perimeter of a square with diagonal 24 cm. [Take √2 = 1.41 ]
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
Find the area of the quadrilateral whose vertices are at (– 9, 0), (– 8, 6), (– 1, – 2) and (– 6, – 3)
The quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio