Advertisements
Advertisements
प्रश्न
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
उत्तर
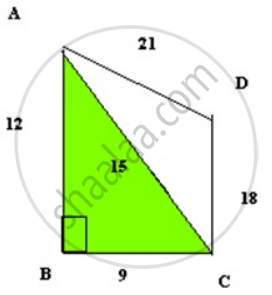
In the given quadrilateral ABCD, join diagonal AC
ABC is a right triangle
We know that, Area of a Triangle = `(1)/(2)"b.h" "i.e" (1)/(2)("Base" xx "Height")`
Area of a Triangle ABC = `(1)/(2)9.12` = 54m2
AC is the hypotenuse, AC
= `sqrt(12^2 + 9^2)`
= `sqrt(225)`
= 15m
Triangle ACD has sides 15m, 18m, 21m
We know that, Area of a Triangle whose sides are a, b, and c and semiperimeter is s is given by `sqrt("s"("s" - "a")("s" - "b")("s" -"c")); "s" = ("a" + "b" + "c")/(2)`
For a triangle whose sides are cm, cm and cm
i.e a = 15, b = 18 and c = 21,
s = `(15 + 18 + 21)/(2)`
= `(54)/(2)`
= 27
Area
= `sqrt(27(27 - 15)(27 - 18)(27 - 21)`
= `sqrt(27(12)(9)(6)`
= `sqrt(9 xx 3(6 xx 2)(9)(6)`
= `9 xx 6sqrt(6)`
= `54sqrt(6)`
= 54(2.5)
Area(Quad ABCD) = Ar(Triangle ABC) + Ar(Triangle ADC)
54 + 54(2.5)
= 54(1 + 2.5)
= 54(3.5)
= 189m2.
APPEARS IN
संबंधित प्रश्न
The distance between parallel sides of a trapezium is 15 cm and the length of the line segment joining the mid-points of its non-parallel sides is 26 cm. Find the area of the trapezium.
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
A wire when bent in the form of a square encloses an area = 576 cm2. Find the largest area enclosed by the same wire when bent to form;
(i) an equilateral triangle.
(ii) A rectangle whose adjacent sides differ by 4 cm.
ABCD is a square with each side 12 cm. P is a point on BC such that area of ΔABP: area of trapezium APCD = 1: 5. Find the length of CP.
Trapezium given below; find its area.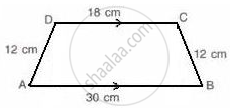
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
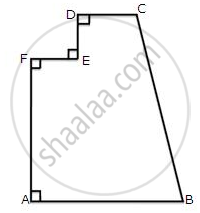
The figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 cm, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (p, p), (5, 6), (5, –2) | 32 |
