Advertisements
Advertisements
प्रश्न
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (p, p), (5, 6), (5, –2) | 32 |
उत्तर
Let the vertices be A(p, p), B(5, 6) and C(5, –2)
Area of a triangle = 32 sq. units
`1/2[(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)]` = 32
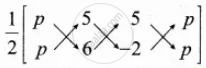
`1/2[(6"p" - 10 + 5"p") - (5"p" + 30 - 2"p")]` = 32
`1/2 [11"p" - 10 - 3"p" - 30]` = 32
11p – 10 – 3p – 30 = 64
8p – 40 = 64
8p = 64 + 40
⇒ 8p = 104
p = `104/8`
= 13
The value of p = 13
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.
The area of a parallelogram is y cm2 and its height is h cm. The base of another parallelogram is x cm more than the base of the first parallelogram and its area is twice the area of the first. Find, in terms of y, h, and x, the expression for the height of the second parallelogram.
A rectangular plot of land measures 45 m x 30 m. A boundary wall of height 2.4 m is built all around the plot at a distance of 1 m from the plot. Find the area of the inner surface of the boundary wall.
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
The perimeter of a rhombus is 52 cm. If one diagonal is 24 cm; find:
(i) The length of its other diagonal,
(ii) Its area.
Two adjacent sides of a parallelogram are 24 cm and 18 cm. If the distance between the longer sides is 12 cm; find the distance between the shorter sides.
In the following, find the value of ‘a’ for which the given points are collinear
(2, 3), (4, a) and (6, – 3)
When proving that a quadrilateral is a parallelogram by using slopes you must find
If vertices of a quadrilateral are at A(– 5, 7), B(– 4, k), C(– 1, – 6) and D(4, 5) and its area is 72 sq. units. Find the value of k.
