Advertisements
Advertisements
Question
Vertices of given triangles are taken in order and their areas are provided aside. Find the value of ‘p’.
| Vertices | Area (sq.units) |
| (p, p), (5, 6), (5, –2) | 32 |
Solution
Let the vertices be A(p, p), B(5, 6) and C(5, –2)
Area of a triangle = 32 sq. units
`1/2[(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)]` = 32
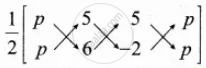
`1/2[(6"p" - 10 + 5"p") - (5"p" + 30 - 2"p")]` = 32
`1/2 [11"p" - 10 - 3"p" - 30]` = 32
11p – 10 – 3p – 30 = 64
8p – 40 = 64
8p = 64 + 40
⇒ 8p = 104
p = `104/8`
= 13
The value of p = 13
APPEARS IN
RELATED QUESTIONS
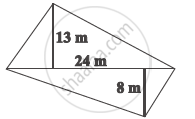
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
ABCD is a square with each side 12 cm. P is a point on BC such that area of ΔABP: area of trapezium APCD = 1: 5. Find the length of CP.
Trapezium given below; find its area.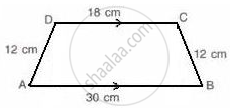
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
The perimeter of a semicircular plate is 108 cm. find its area.
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
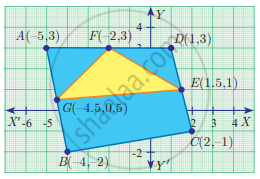
Find the area of quadrilateral BCEG