Advertisements
Advertisements
Question
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
Solution
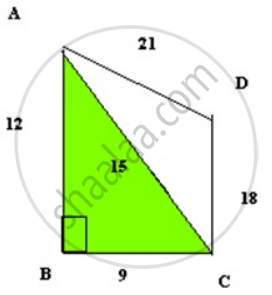
In the given quadrilateral ABCD, join diagonal AC
ABC is a right triangle
We know that, Area of a Triangle = `(1)/(2)"b.h" "i.e" (1)/(2)("Base" xx "Height")`
Area of a Triangle ABC = `(1)/(2)9.12` = 54m2
AC is the hypotenuse, AC
= `sqrt(12^2 + 9^2)`
= `sqrt(225)`
= 15m
Triangle ACD has sides 15m, 18m, 21m
We know that, Area of a Triangle whose sides are a, b, and c and semiperimeter is s is given by `sqrt("s"("s" - "a")("s" - "b")("s" -"c")); "s" = ("a" + "b" + "c")/(2)`
For a triangle whose sides are cm, cm and cm
i.e a = 15, b = 18 and c = 21,
s = `(15 + 18 + 21)/(2)`
= `(54)/(2)`
= 27
Area
= `sqrt(27(27 - 15)(27 - 18)(27 - 21)`
= `sqrt(27(12)(9)(6)`
= `sqrt(9 xx 3(6 xx 2)(9)(6)`
= `9 xx 6sqrt(6)`
= `54sqrt(6)`
= 54(2.5)
Area(Quad ABCD) = Ar(Triangle ABC) + Ar(Triangle ADC)
54 + 54(2.5)
= 54(1 + 2.5)
= 54(3.5)
= 189m2.
APPEARS IN
RELATED QUESTIONS
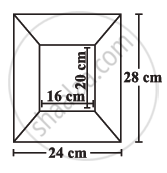
Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.
A rectangular plot of land measures 45 m x 30 m. A boundary wall of height 2.4 m is built all around the plot at a distance of 1 m from the plot. Find the area of the inner surface of the boundary wall.
Trapezium given below; find its area.

A triangle and a parallelogram have the same base and the same area. If the side of the triangle is 26 cm, 28 cm, and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
The perimeter of a semicircular plate is 108 cm. find its area.
Find the area of the quadrilateral whose vertices are at (– 9, 0), (– 8, 6), (– 1, – 2) and (– 6, – 3)
Let P(11, 7), Q(13.5, 4) and R(9.5, 4) be the midpoints of the sides AB, BC and AC respectively of ∆ABC. Find the coordinates of the vertices A, B and C. Hence find the area of ∆ABC and compare this with area of ∆PQR.
The quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio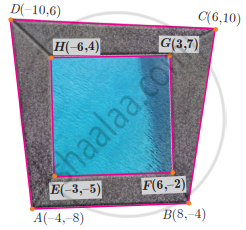
When proving that a quadrilateral is a parallelogram by using slopes you must find
If vertices of a quadrilateral are at A(– 5, 7), B(– 4, k), C(– 1, – 6) and D(4, 5) and its area is 72 sq. units. Find the value of k.
