Advertisements
Advertisements
Question
Let P(11, 7), Q(13.5, 4) and R(9.5, 4) be the midpoints of the sides AB, BC and AC respectively of ∆ABC. Find the coordinates of the vertices A, B and C. Hence find the area of ∆ABC and compare this with area of ∆PQR.
Solution
Let the vertices of the ∆ABC be A(x1, y1), B(x2, y2), C(x3, y3)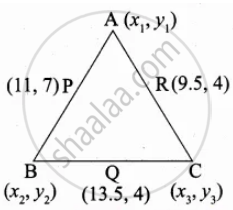
Mid point of AB = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
(11, 7) = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
|
`(x_1 + x_2)/2` = 11 x1 + x2 = 22 ...(1) |
`(y_1 + y_2)/2` = 7 y1 + y2 = 14 ...(2) |
Mid point of BC = `((x_2 + x_3)/2, (y_2 + y_3)/2)`
⇒ (13.5, 4) = `((x_2 + x_3)/2, (y_2 + y_3)/2)`
|
`(x_2 + x_3)/2` = 13.5 x2 + x3 = 27 ...(3) |
`(y_2 + y_3)/2` = 4 y2 + y3 = 8 ...(4) |
Mid point of AC = `((x_1 + x_3)/2, (y_1 + y_3)/2)`
(9.5, 4) = `((x_1 + x_2)/2, (y_1 + y_3)/2)`
|
`(x_1 + x_3)/2` = 9.5 x1 + x3 = 19 ...(5) |
`(y_1 + y_3)/2` = 4 y1 + y3 = 8 ...(6) |
Add (1), (3) and (5)
2x1 + 2x2 + 2x3 = 22 + 27 + 19
2(x1 + x2 + x3) = 68
x1 + x2 + x3 = 34
From (1) ⇒ x1 + x2 = 22
x3 = 34 – 22 = 12
From (3) ⇒ x2 + x3 = 27
x1 = 34 – 27 = 7
From (5) ⇒ x1 + x3 = 19
x2 = 34 – 19 = 15
Add (2), (4) and (6)
2y1 + 2y2 + 2y3 = 14 + 8 + 8
2(y1 + y2 + y3) = 30
y1 + y2 + y3 = 15
From (2) ⇒ y1 + y2 = 14
y3 = 15 – 14 = 1
From (4) ⇒ y2 + y3 = 18
y1 = 15 – 8 = 7
From (6) ⇒ y1 + y3 = 8
y2 = 15 – 8 = 7
The vertices of a ΔABC are A(7, 7), B(15, 7) and C(12, 1)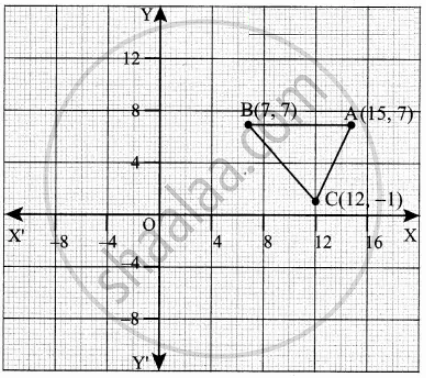
Area of ΔABC = `1/2[(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)]`

= `1/2[(7 + 84 + 105) - (84 + 15 + 49)]`
= `1/2[196 - 148]`
= `1/2 xx 48`
= 24 sq. units
Area of ΔPRQ = `1/2[(44 + 8 + 94.5) - (66.5 + 54 + 44)]`
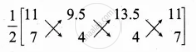
= `1/2[176.5 - 164.5]`
= `1/2 xx 12`
= 6 sq. units
APPEARS IN
RELATED QUESTIONS
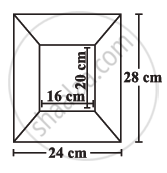
Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.
The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.
The figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 cm, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
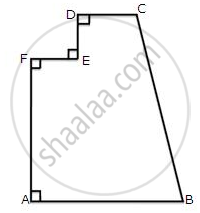
Two adjacent sides of a parallelogram are 24 cm and 18 cm. If the distance between the longer sides is 12 cm; find the distance between the shorter sides.
A floor that measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm. Find the number of tiles required.
Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is left uncovered?
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
Find the area of the quadrilateral whose vertices are at (– 9, – 2), (– 8, – 4), (2, 2) and (1, – 3)
The quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio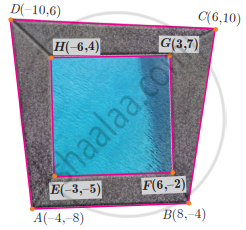
Find the area of quadrilateral BCEG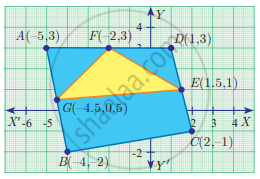
When proving that a quadrilateral is a parallelogram by using slopes you must find
