Advertisements
Advertisements
Question
When proving that a quadrilateral is a parallelogram by using slopes you must find
Options
The slopes of two sides
The slopes of two pair of opposite sides
The lengths of all sides
Both the lengths and slopes of two sides
Solution
When proving that a quadrilateral is a parallelogram by using slopes you must find The slopes of two pair of opposite sides
APPEARS IN
RELATED QUESTIONS
The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.
The area of a rectangular is 640 m2. Taking its length as x cm; find in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm ∠A = 90° and BC = CD = 52 cm.
A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to from:
- An equilateral triangle.
- A rectangle of length 16 m.
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and the area is 3 times that of the rectangle.
The area of a rhombus is 216 sq. cm. If it's one diagonal is 24 cm; find:
(i) Length of its other diagonal,
(ii) Length of its side,
(iii) The perimeter of the rhombus.
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.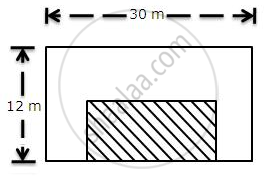
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 meters. Given your answer correct to 2 places of decimals.
Find the area of quadrilateral BCEG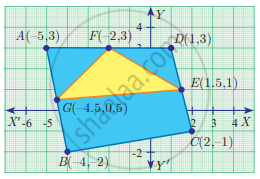
PQRS is a rectangle formed by joining the points P(– 1, – 1), Q(– 1, 4), R(5, 4) and S(5, – 1). A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.
