Advertisements
Advertisements
Question
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn, there are flowerbeds having a uniform width of 2 m.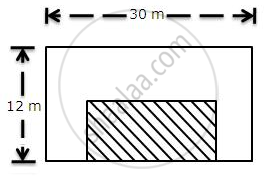
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
Solution
Consider the following figure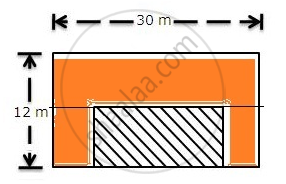
(i) The length of the lawn = 30 - 2 - 2 = 26 m
The breadth of the lawn = 12 - 2 = 10 m
(ii) The orange shaded area in the figure is the required area.
Area of the flower bed is calculated as follows:
A = 10 x 2 + 10 x 2 + 30 x 2
= 20 + 20 + 60
= 100 sq.m.
APPEARS IN
RELATED QUESTIONS
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
A wire when bent in the form of a square encloses an area = 576 cm2. Find the largest area enclosed by the same wire when bent to form;
(i) an equilateral triangle.
(ii) A rectangle whose adjacent sides differ by 4 cm.
The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.
Trapezium given below; find its area.

How many tiles, each of area 400 cm2, will be needed to pave a footpath which is 2 m wide and surrounds a grass plot 25 m long and 13 m wide?
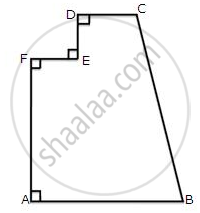
The figure given below shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 cm, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
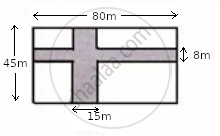
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
Find the diagonal of a quadrilateral whose area is 756cm2 and the perpendicular from the opposite vertices are 17cm and 19cm.
Find the area of the quadrilateral whose vertices are at (– 9, – 2), (– 8, – 4), (2, 2) and (1, – 3)
When proving that a quadrilateral is a trapezium, it is necessary to show
