Advertisements
Advertisements
Question
A wire when bent in the form of a square encloses an area = 576 cm2. Find the largest area enclosed by the same wire when bent to form;
(i) an equilateral triangle.
(ii) A rectangle whose adjacent sides differ by 4 cm.
Solution
Let a be the length of each side.
a2 = 576
a = 24 cm
4a = 96 cm
Hence length of the wire = 96 cm
(i) For the equilateral triangle,
side = `96/3` = 32 cm
Area = `sqrt3/4`( side )2
= `sqrt3/4` x 322
= 256√3 sq.cm
(ii) Let the adjacent side of the rectangle be x and y cm.
Since the perimeter is 96 cm, we have,
2( x + y ) = 96
Hence,
x + y = 48
x - y = 4
x = 26
y = 22
Hence area of the rectangle is = 26 x 22 = 572 sq.cm
APPEARS IN
RELATED QUESTIONS
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
Trapezium given below; find its area.
Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm ∠A = 90° and BC = CD = 52 cm.
Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.
A triangle and a parallelogram have the same base and the same area. If the side of the triangle is 26 cm, 28 cm, and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
A quadrilateral field of unequal has a longer diagonal with 140m. The perpendiculars from opposite vertives upon this diagonal are 20m and 14m. Find the area of the field.
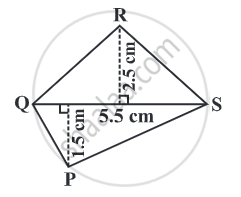
Find the area of quadrilateral PQRS.
Find the area of the quadrilateral whose vertices are at (– 9, 0), (– 8, 6), (– 1, – 2) and (– 6, – 3)
Let P(11, 7), Q(13.5, 4) and R(9.5, 4) be the midpoints of the sides AB, BC and AC respectively of ∆ABC. Find the coordinates of the vertices A, B and C. Hence find the area of ∆ABC and compare this with area of ∆PQR.
Find the area of quadrilateral BCEG