Advertisements
Advertisements
Question
A quadrilateral field of unequal has a longer diagonal with 140m. The perpendiculars from opposite vertives upon this diagonal are 20m and 14m. Find the area of the field.
Solution
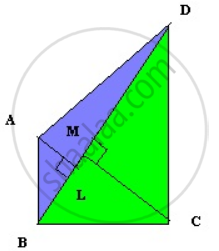
In quadrilateral ABCD, the sides AB, BC, CD and AD are unequal.
The longer diagonal BD = 140m
AM ⊥ BD, CL ⊥ BD
AM = 20m and CL = 14m.
We split a quadrilateral into triangles and find its area.
We know that,
Area of a Triangle = `(1)/(2)"b.h" "i.e" (1)/(2)("Base" xx "Height")`
Ar(ΔABD) = `(1)/(2)"BD" xx "AL";(Δ"CBD") = (1)/(2)"BD" xx "CM"`
Ar(QuadABCD) = Ar(ΔABD) + Ar(ΔCBD)
= `(1)/(2)"BD" xx "AL" + (1)/(2)"BD" xx "CM"`
= `(1)/(2)"BD" xx ("AL" + "CM")`
= `(1)/(2) xx 140 xx (20 + 14)`
= 70 x 34
= 2380m2.
APPEARS IN
RELATED QUESTIONS
The area of a rectangular is 640 m2. Taking its length as x cm; find in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.
The perimeter of a rectangular field is `3/5`km. If the length of the field is twice its width; find the area of the rectangle in sq. meters.
Calculate the area of the figure given below: which is not drawn scale.
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
The area of a rhombus is 216 sq. cm. If it's one diagonal is 24 cm; find:
(i) Length of its other diagonal,
(ii) Length of its side,
(iii) The perimeter of the rhombus.
Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 meters. Given your answer correct to 2 places of decimals.
Find the area of a quadrilateral field whose sides are 12m, 9m, 18m and 21m respectively and the angle between the first two sides is a right angle. Take the value of `sqrt(6)` as 2.5.
Find the diagonal of a quadrilateral whose area is 756cm2 and the perpendicular from the opposite vertices are 17cm and 19cm.
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ______.
