Advertisements
Advertisements
Question
The area of a rectangular is 640 m2. Taking its length as x cm; find in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
Solution
Let b be the width of the rectangle.
`x` x b = 640
b = `640/x`
Again perimeter of the rectangle is 104 m.
Hence,
`2( x + 640/x )` = 104
x2 - 52x + 640 = 0
( x - 32 )( x - 20 ) = 0
x = 32, 20.
Hence
length = 32 m
width = 20 m.
APPEARS IN
RELATED QUESTIONS
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
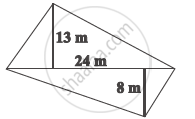
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
Trapezium given below; find its area.

A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to from:
- An equilateral triangle.
- A rectangle of length 16 m.
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH, and HD are 50 m, 40 m, 15 m and 25 m, respectively, and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.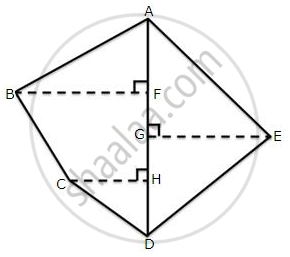
Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 meters. Given your answer correct to 2 places of decimals.
Using the information in the following figure, find its area.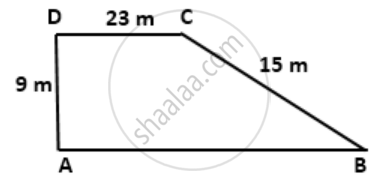
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (– 4, – 2), (– 3, k), (3, – 2) and (2, 3)
